If in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
To solve the problem, we need to determine the relationship between the two triangles ABC and DEF given the proportional sides:
ABDE=BCFE=CAFD
This indicates that the triangles are similar by the Side-Side-Side (SSS) similarity criterion.
1. Understanding the Proportionality:
We have the ratios of the corresponding sides of triangles ABC and DEF being equal. This means that the triangles are similar.
2. Using the Similarity:
Since the triangles are similar, the corresponding angles of the triangles will also be equal. Therefore, we can denote:
- ∠A=∠D
- ∠B=∠E
- ∠C=∠F
3. Identifying the Corresponding Vertices:
From the similarity, we can conclude that the order of the vertices in the triangles corresponds to the order of the angles:
- If ∠A corresponds to ∠D, then A corresponds to D.
- If ∠B corresponds to ∠E, then B corresponds to E.
- If ∠C corresponds to ∠F, then C corresponds to F.
4. Writing the Correspondence:
Therefore, we can write the correspondence of the triangles as:
ABC∼DEF
This means that the vertices can be arranged in the following way:
- A corresponds to D
- B corresponds to E
- C corresponds to F
5. Choosing the Correct Option:
Based on the correspondence established, we can express the similarity in terms of the options provided:
- The correct arrangement that reflects the similarity is ABC corresponding to DEF.
Thus, the answer is:
(b) FDEABC
We have the ratios of the corresponding sides of triangles ABC and DEF being equal. This means that the triangles are similar.
Since the triangles are similar, the corresponding angles of the triangles will also be equal. Therefore, we can denote:
- ∠A=∠D
- ∠B=∠E
- ∠C=∠F
From the similarity, we can conclude that the order of the vertices in the triangles corresponds to the order of the angles:
- If ∠A corresponds to ∠D, then A corresponds to D.
- If ∠B corresponds to ∠E, then B corresponds to E.
- If ∠C corresponds to ∠F, then C corresponds to F.
Therefore, we can write the correspondence of the triangles as:
ABC∼DEF
This means that the vertices can be arranged in the following way:
- A corresponds to D
- B corresponds to E
- C corresponds to F
Based on the correspondence established, we can express the similarity in terms of the options provided:
- The correct arrangement that reflects the similarity is ABC corresponding to DEF.
(b) FDEABC
Topper's Solved these Questions
Similar Questions
Knowledge Check
ab=cd=ef=k(a,b,c,d,e,f>0) then
Ak=a+c+eb+d+fBk=a2+c2+e2b2+d2+f2Ck=c2e2d2f2Dk=(acebdf)13
In Fig. 71, if ABCD and CDEF, find ∠ACE
View Solution
Identify A, B, C, D, E, F,G
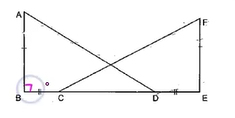
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionMost A, B, C, D, E and F refer to

View SolutionWhich of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View Solution