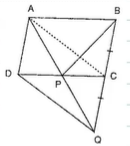
In Figure, ABCD and P is any point shown in the figure. Prove that: ∠ABP+∠BPD+∠CDP=360∘
AB II CO II EF' (By Construction)
⇒ '∠ABP+∠EPB=180°-------(1)'(co-interior angles are supplementry)
⇒'∠CDP+∠EPD=180° --------(2) '(co-interior angles are supplementry)
Add equation '(1)' and '(2)',
⇒(∠ABP+∠CDP+∠EPB+∠EPD=180°+180°)
⇒∠ABP+∠CDP+∠BPD=360°
Topper's Solved these Questions
Similar Questions
In Figure, ABCD and P is any point shown in the figure. Prove that: ∠ABP+∠BPD+∠CDP=360∘
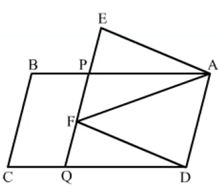
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
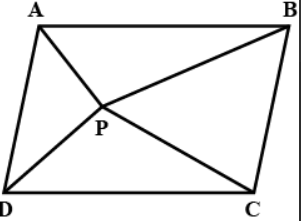
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View Solution