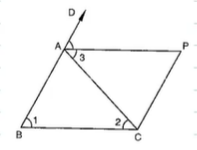
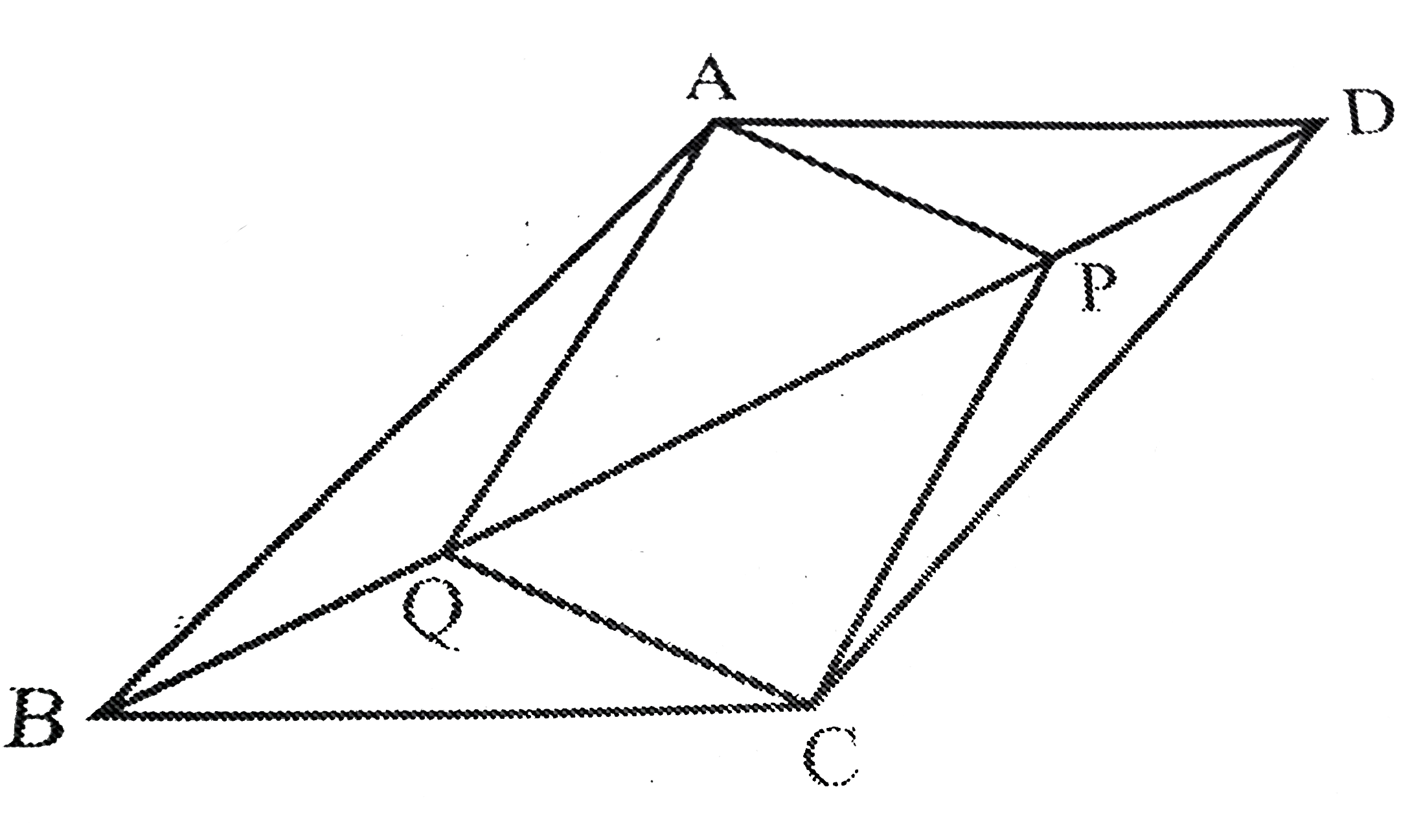
In figure and is the bisector of exterior of . Prove that (ii) is a parallelogram
Step by step video & image solution for In figure A B=A C\ a n d\ C P||B A and A P is the bisector of exterior /_C A D of A B C . Prove that /_P A C=/_B C A (ii) A B C P is a parallelogram by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
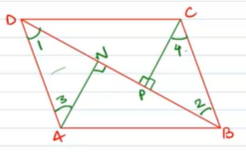
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
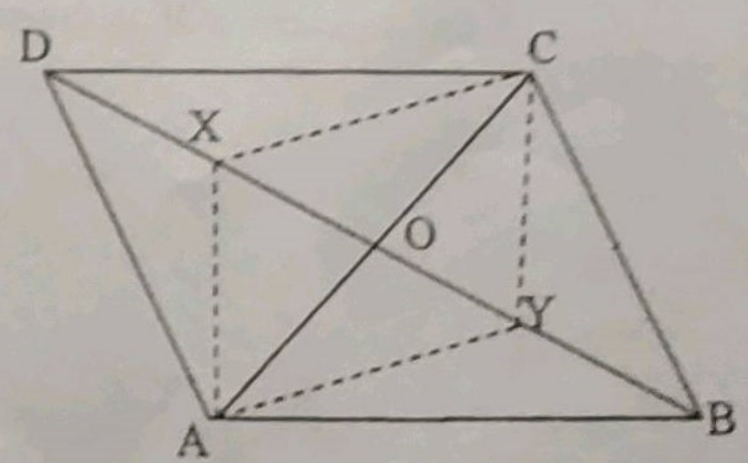
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
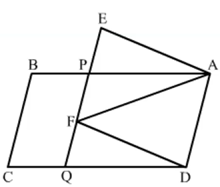
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionIn figure D is a point on side BC of a ΔABCsuch that BDCD=ABAC. Prove that AD is the bisector of ∠BAC.

View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.
View Solution
