In Figure, if QT⊥PR, ∠TQR=400 and ∠SPR=300, find x and y.
Consider right △QTR ,
Where,∠T=90o
[QT⊥PR]
Sum of all the angles of a triangle is180o
Hence, ∠RQT+∠QTS+∠TRQ=180o⇒40o+90o+∠R=180o<BR>∠TRS=180o−130o=50o
Now, ∠PSQ=∠SPR+∠PRS (Exterior angle is equal to sum of interior opposite angles.)
∠PSQ=30o+50o=80o
Topper's Solved these Questions
Similar Questions
In Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.
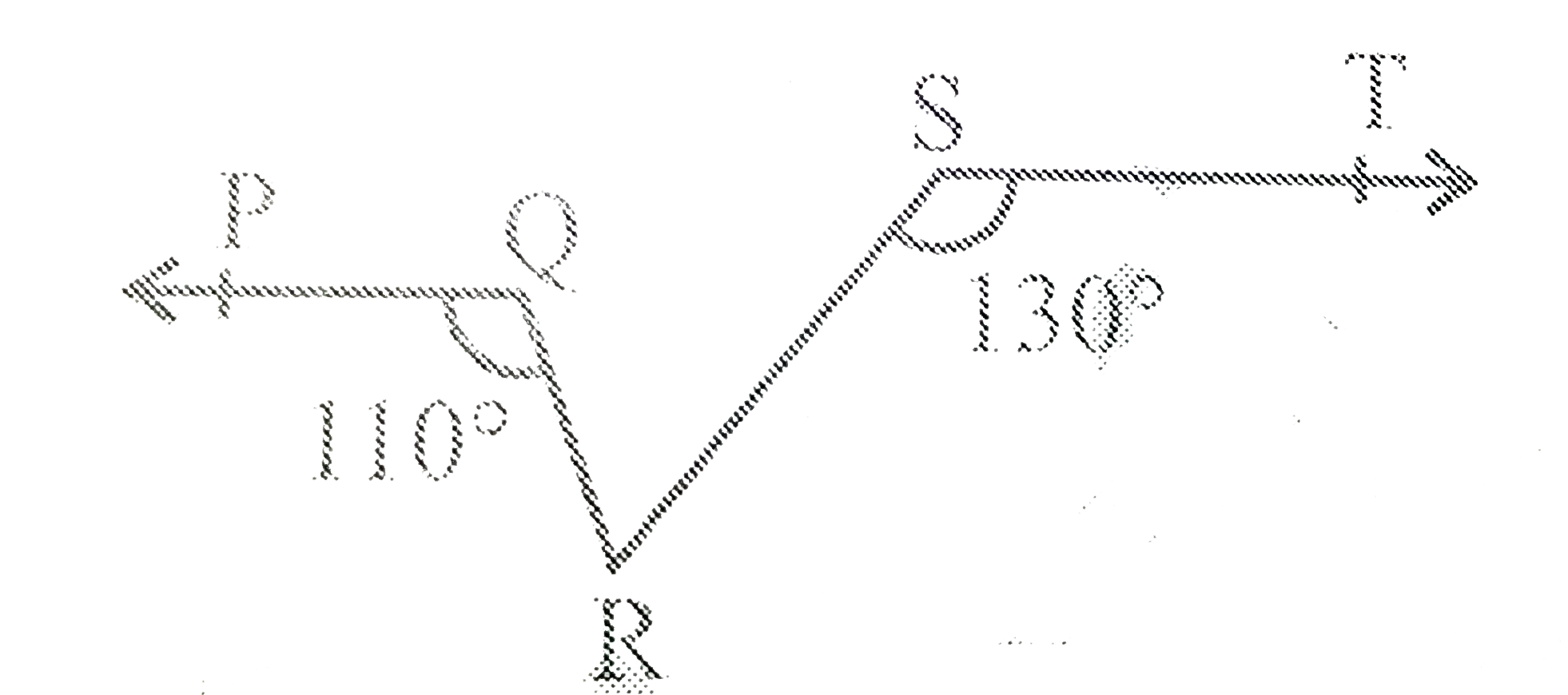 View Solution
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
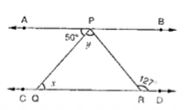 View Solution
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
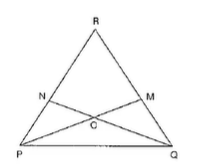 View Solution
View SolutionIn Fig. 6.24, if PQ∣∣RS,∠MXQ=135∘ and∠MYR=40∘, find∠XMY..
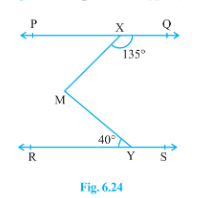 View Solution
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.
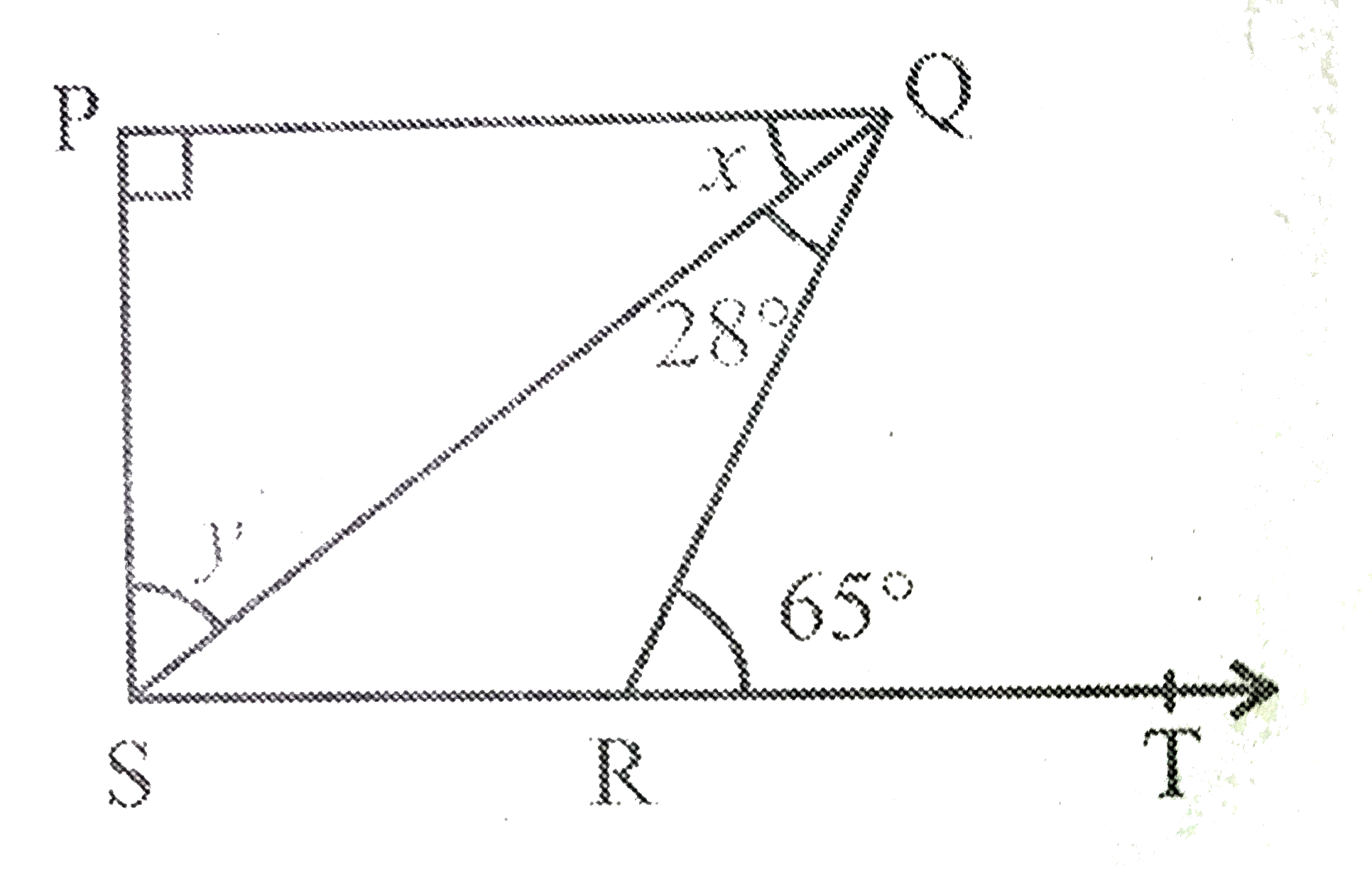 View Solution
View SolutionIn Fig.103, PQRS and ∠PAB=600 and ∠ACS=1000. Then, ∠BAC= (a) (b)(c)(d)(e)40(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)60(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)80(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)50(q)0(r)(s)(t) (u)
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
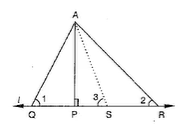 View Solution
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionIn Figure, PQRS is a parallelogram. If XandY are mid-points of PQandSR respectively and diagonal SQ is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=
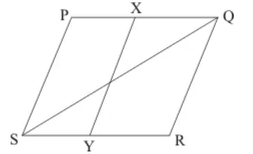
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1View SolutionIn Figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT=1520, find x, y and z
 View Solution
View Solution

