In a triangle if is produced to such that find
To solve the problem, we will follow these steps:
Step 1: Understand the Triangle and Given Conditions
We have a triangle ABC where AB=AC. This means that triangle ABC is isosceles with angles ∠ABC=∠ACB.
Step 2: Define Angles
Let ∠ABC=∠ACB=X. Since AB is produced to D such that BD=BC, we need to find the angles ∠ACD and ∠ADC.
Step 3: Identify Linear Pair
Since AB is extended to D, we have the linear pair ∠ABC+∠DBC=180∘. Thus, we can write:
∠DBC=180∘−∠ABC=180∘−X
Step 4: Analyze Triangle DBC
In triangle DBC, we know:
∠DBC+∠BDC+∠BCA=180∘
Substituting the known angles:
(180∘−X)+∠BDC+X=180∘
This simplifies to:
∠BDC=X
Step 5: Identify Angles in Triangle DBC
Since BD=BC, triangle DBC is isosceles with ∠BDC=∠BCD=Y. Therefore, we can write:
∠BDC+∠BCD+∠DBC=180∘
Substituting the angles:
Y+Y+(180∘−X)=180∘
This simplifies to:
2Y+180∘−X=180∘
Thus:
2Y=X⟹Y=X2
Step 6: Find Angles ∠ACD and ∠ADC
Now we can find:
- ∠ACD=∠ABC+∠BCD=X+Y=X+X2=3X2
- ∠ADC=Y=X2
Step 7: Calculate the Ratio
Now, we find the ratio of ∠ACD to ∠ADC:
∠ACD∠ADC=3X2X2=3X2⋅2X=3
Thus, the ratio is:
Ratio of ∠ACD:∠ADC=3:1
Final Answer
The required ratio ∠ACD:∠ADC is 3:1.
---
We have a triangle ABC where AB=AC. This means that triangle ABC is isosceles with angles ∠ABC=∠ACB.
Let ∠ABC=∠ACB=X. Since AB is produced to D such that BD=BC, we need to find the angles ∠ACD and ∠ADC.
Since AB is extended to D, we have the linear pair ∠ABC+∠DBC=180∘. Thus, we can write:
∠DBC=180∘−∠ABC=180∘−X
In triangle DBC, we know:
∠DBC+∠BDC+∠BCA=180∘
Substituting the known angles:
(180∘−X)+∠BDC+X=180∘
This simplifies to:
∠BDC=X
Since BD=BC, triangle DBC is isosceles with ∠BDC=∠BCD=Y. Therefore, we can write:
∠BDC+∠BCD+∠DBC=180∘
Substituting the angles:
Y+Y+(180∘−X)=180∘
This simplifies to:
2Y+180∘−X=180∘
Thus:
2Y=X⟹Y=X2
Now we can find:
- ∠ACD=∠ABC+∠BCD=X+Y=X+X2=3X2
- ∠ADC=Y=X2
Now, we find the ratio of ∠ACD to ∠ADC:
∠ACD∠ADC=3X2X2=3X2⋅2X=3
Thus, the ratio is:
Ratio of ∠ACD:∠ADC=3:1
The required ratio ∠ACD:∠ADC is 3:1.
Topper's Solved these Questions
Similar Questions
Any point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
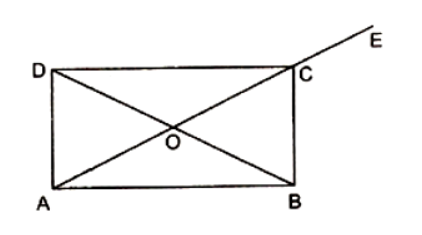
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC

View SolutionSide BC of a triangle ABC has been produced to a point D such that ∠1200. If ∠B=12∠A, then ∠A is equal to 800 (b) 750 (c) 600 (d) 900
View SolutionThe side BC of ABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=300and ∠ACD=1150, then ∠ALC= 850 (b) 72120 (c) 1450 (d) none of these
View SolutionIn Fig. 4.124, E is a point on side CB produced of an isosceles triangle ABC with AB=AC . If AD⊥BC and EF⊥AC , prove that (i) ABDECF (ii) AB×EF=AD×EC . (FIGURE)
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
View SolutionD is a point on the side BC of ABC. A line PDQ , though D , meets side AC in P and AB produced at Q . If ∠A=800, ∠ABC=600 and ∠PDC=150 find (i) ∠AQD (ii) ∠APD.
View Solution
