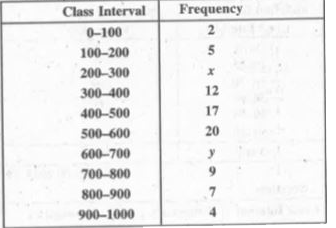
The median of the following data is 525. Find the values of x and y , if the total frequency is 100 Class interval Frequency 0 100 2 100 200 5 200 300 x 300 400 12 400 500 17 500 600 20 600 700 y 700 800 9 800 900 7 900 1000 4
To solve the problem step by step, we need to find the values of x and y given that the median of the data is 525 and the total frequency is 100.
Step 1: Calculate the cumulative frequency (cf)
We need to find the cumulative frequency for each class interval. The cumulative frequency is the sum of the frequencies of all preceding classes.
| Class Interval | Frequency | Cumulative Frequency (cf) |
|----------------|-----------|----------------------------|
| 0 - 100 | 2 | 2 |
| 100 - 200 | 5 | 2 + 5 = 7 |
| 200 - 300 | x | 7 + x |
| 300 - 400 | 12 | 7 + x + 12 |
| 400 - 500 | 17 | 7 + x + 12 + 17 |
| 500 - 600 | 20 | 7 + x + 12 + 17 + 20 |
| 600 - 700 | y | 7 + x + 12 + 17 + 20 + y |
| 700 - 800 | 9 | 7 + x + 12 + 17 + 20 + y + 9 |
| 800 - 900 | 7 | 7 + x + 12 + 17 + 20 + y + 9 + 7 |
| 900 - 1000 | 4 | 7 + x + 12 + 17 + 20 + y + 9 + 7 + 4 |
The total frequency is given as 100, so we can set up the equation:
2+5+x+12+17+20+y+9+7+4=100
Step 2: Simplify the equation
Calculating the known frequencies:
2+5+12+17+20+9+7+4=76
So, we have:
76+x+y=100
This simplifies to:
x+y=100−76
x+y=24 (Equation 1)
Step 3: Identify the median class
The median is given as 525. To find the median class, we need to find the cumulative frequency just greater than n/2, where n=100:
n/2=50
Looking at the cumulative frequencies:
- The cumulative frequency just before 50 is 36 (from the class 400 - 500).
- The cumulative frequency for the class 500 - 600 is 36+20=56.
Thus, the median class is 500 - 600.
Step 4: Apply the median formula
The formula for the median is:
Median=l+(n/2−cff)×h
Where:
- l=500 (lower boundary of the median class)
- n=100
- cf=36+x (cumulative frequency of the class before the median class)
- f=20 (frequency of the median class)
- h=100 (class width)
Substituting the values into the formula:
525=500+(50−(36+x)20)×100
Step 5: Solve for x
Rearranging gives:
525−500=(50−(36+x)20)×100
25=(50−36−x20)×100
25=14−x20×100
25=5(14−x)
25=70−5x
5x=70−25
5x=45
x=9
Step 6: Find y
Using Equation 1:
x+y=24
Substituting x=9:
9+y=24
y=24−9
y=15
Final Values
Thus, the values of x and y are:
- x=9
- y=15
We need to find the cumulative frequency for each class interval. The cumulative frequency is the sum of the frequencies of all preceding classes.
|----------------|-----------|----------------------------|
| 0 - 100 | 2 | 2 |
| 100 - 200 | 5 | 2 + 5 = 7 |
| 200 - 300 | x | 7 + x |
| 300 - 400 | 12 | 7 + x + 12 |
| 400 - 500 | 17 | 7 + x + 12 + 17 |
| 500 - 600 | 20 | 7 + x + 12 + 17 + 20 |
| 600 - 700 | y | 7 + x + 12 + 17 + 20 + y |
| 700 - 800 | 9 | 7 + x + 12 + 17 + 20 + y + 9 |
| 800 - 900 | 7 | 7 + x + 12 + 17 + 20 + y + 9 + 7 |
| 900 - 1000 | 4 | 7 + x + 12 + 17 + 20 + y + 9 + 7 + 4 |
2+5+x+12+17+20+y+9+7+4=100
Calculating the known frequencies:
2+5+12+17+20+9+7+4=76
76+x+y=100
This simplifies to:
x+y=100−76
x+y=24 (Equation 1)
The median is given as 525. To find the median class, we need to find the cumulative frequency just greater than n/2, where n=100:
n/2=50
- The cumulative frequency just before 50 is 36 (from the class 400 - 500).
- The cumulative frequency for the class 500 - 600 is 36+20=56.
The formula for the median is:
Median=l+(n/2−cff)×h
Where:
- l=500 (lower boundary of the median class)
- n=100
- cf=36+x (cumulative frequency of the class before the median class)
- f=20 (frequency of the median class)
- h=100 (class width)
525=500+(50−(36+x)20)×100
Rearranging gives:
525−500=(50−(36+x)20)×100
25=(50−36−x20)×100
25=14−x20×100
25=5(14−x)
25=70−5x
5x=70−25
5x=45
x=9
Using Equation 1:
x+y=24
Substituting x=9:
9+y=24
y=24−9
y=15
Thus, the values of x and y are:
- x=9
- y=15
Topper's Solved these Questions
Similar Questions
The median of the following data is 525. find the the value of x and y, if the total frequency is 100 :
View SolutionThe median of the following dats is 52.5. If the total frequency is 100, find the value of x and y
View SolutionThe median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data: Class interval Frequency Class interval Frequency 0 100 2 500 600 20 100 200 5 600 700 f2 200 300 f1 700 800 9 300 400 12 800 900 7 400 500 17 900 1000 4
View SolutionIf the median of the following frequency distribution is 525, in the table given below, find the value of x and y. if total frequency is 100.

View SolutionIf the median of the following data is 32.5, find the missing frequencies. Class interval: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Total Frequency: f1 5 9 12 f2 3 2 40
View SolutionIf the mean of the following data is 26, then find the missing frequency x.
Class Intervalf 0−104 10−20X 20−309 30−405 40−506
View SolutionFind the mean deviation from the mean for the following data: Classes 0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800 Frequencies 4 8 9 10 7 5 4 3
View SolutionFind the mean deviation about the mean for the data : Income 0-100 100-200 200-300 300-400 400-500 500-600 600-700 700-800per dayNumber 4 8 9 10 7 5 4 3of persons
View SolutionFind the median of the following data: class : 0−10,equency:5, 10−20,3, 20−30,4, 30−40,3, 40−50,3,50-60 , 4,60-70 , 7, 70-80 , 9,80-90 , 7,90-100 , 8,
View SolutionA frequency distribution of the life times of 400 T.V. picture tubes tested in a tube company is given below. Find the average life of tube. Life Time (in hrs) Frequency Life time (in hrs) Frequency 300-399 400-499 500-599 600-699 700-799 14 46 58 76 68 800-899 900-999 1000-1099 1100-1199 62 48 22 6
View Solution
