Question

If the median of the distribution given below is 28.5, find the value
of ${\displaystyle x}$
and ${\displaystyle y}$
.
Class interval: 0-10 10-20
20-30 30-40 40-50
50-60
No. of students: 5 ${\displaystyle x}$
20 15 ${\displaystyle y}$
5

Explanation

To solve the problem step by step, we need to find the values of $x$ and $y$ in the given distribution table based on the median value of 28.5.

Step 1: Set Up the Cumulative Frequency Table
The given class intervals and the number of students are as follows:

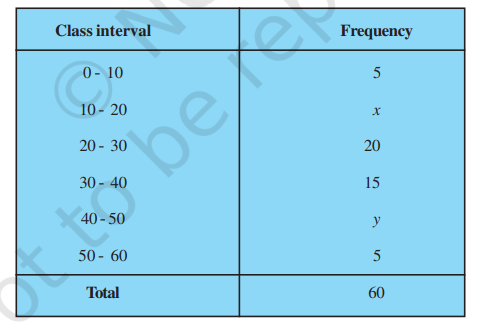
| Class Interval | No. of Students |
|----------------|-----------------|
| 0 - 10 | 5 |
| 10 - 20 | x |
| 20 - 30 | 20 |
| 30 - 40 | 15 |
| 40 - 50 | y |
| 50 - 60 | 5 |

Now, we need to calculate the cumulative frequency (cf):

- For 0 - 10: cf = 5
- For 10 - 20: cf = 5 + x
- For 20 - 30: cf = 5 + x + 20 = 25 + x
- For 30 - 40: cf = 25 + x + 15 = 40 + x
- For 40 - 50: cf = 40 + x + y
- For 50 - 60: cf = 40 + x + y + 5 = 45 + x + y

Step 2: Total Number of Students
The total number of students is given as 60. Therefore, we can set up the equation:

\( 45 + x + y = 60 \)

From this, we can simplify to find:

\( x + y = 15 \)

Step 3: Identify the Median Class
The median is given as 28.5. To find the median class, we calculate \( n/2 \):

\( n/2 = 60/2 = 30 \)

Now we look for the cumulative frequency just greater than 30.

- The cumulative frequency for the class 20-30 is \( 25 + x \).
- The cumulative frequency for the class 30-40 is \( 40 + x \).

Since \( 30 \) falls between these two, the median class is 30-40.

Step 4: Apply the Median Formula
The formula for the median is given by:

\( \text{Median} = l + \left( \frac{n/2 - cf}{f} \right) \times h \)

Where:
- \( l \) = lower boundary of the median class = 30
- \( n \) = total frequency = 60
- \( cf \) = cumulative frequency of the class preceding the median class = \( 25 + x \)
- \( f \) = frequency of the median class = 15
- \( h \) = width of the class interval = 10

Substituting the values into the formula:

\( 28.5 = 30 + \left( \frac{30 - (25 + x)}{15} \right) \times 10 \)

Step 5: Simplify the Equation
Now, simplify the equation:

\( 28.5 = 30 + \left( \frac{5 - x}{15} \right) \times 10 \)

\( 28.5 - 30 = \frac{10(5 - x)}{15} \)

\( -1.5 = \frac{10(5 - x)}{15} \)

Multiply both sides by 15:

\( -22.5 = 10(5 - x) \)

Divide by 10:

\( -2.25 = 5 - x \)

Rearranging gives:

\( x = 5 + 2.25 = 7.25 \)

Step 6: Find y
Now, using the equation from Step 2:

\( x + y = 15 \)
Substituting \( x = 7.25 \):

\( 7.25 + y = 15 \)

Solving for \( y \):

\( y = 15 - 7.25 = 7.75 \)

Final Values
Thus, we find:

- \( x = 7.25 \)
- \( y = 7.75 \)