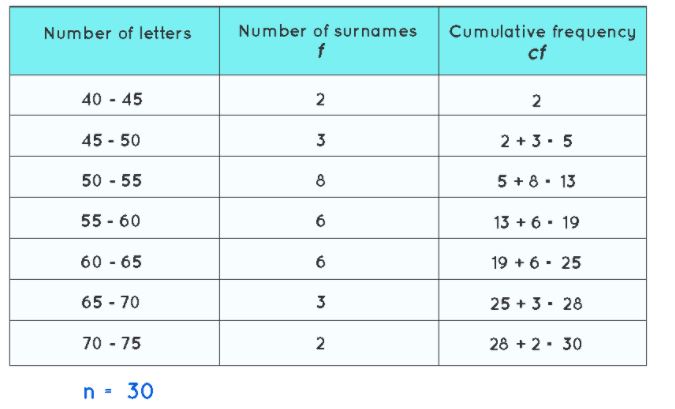
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.
Here,
From the table, it can be observed that cumulative frequency (cf) just greater than 15 is 19, belonging to class 55 - 60.
Therefore, median class =
Class size,
Lower limit of median class,
Frequency of median class,
Cumulative frequency of class preceding median class,
Median
Therefore, median weight is 56.67 kg.
Similar Questions
The distribution below gives the weight of 30 students in a class. Find the median weight of students: Weight (in kg): 40-45 45-50 50-55 55-60 60-65 65-70 70-75 No. of students: 2 3 8 6 6 3 2
View SolutionThe distribution given below show the marks of 100 students of a class:
then find Ogive medium of data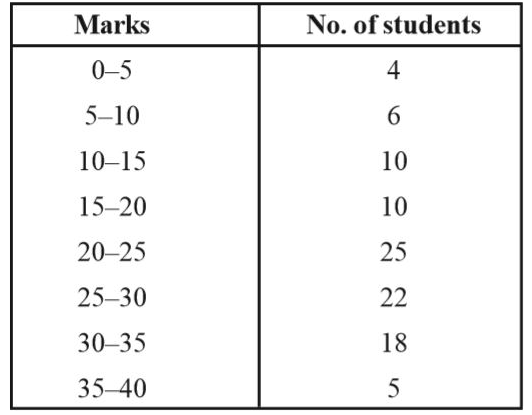 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Consider the following frequency distribution of the height of 60 students of a class:
The upper limit of the median class in the given data is:
 A165B155C160D170
A165B155C160D170
The weight (in kg) of students are given below :
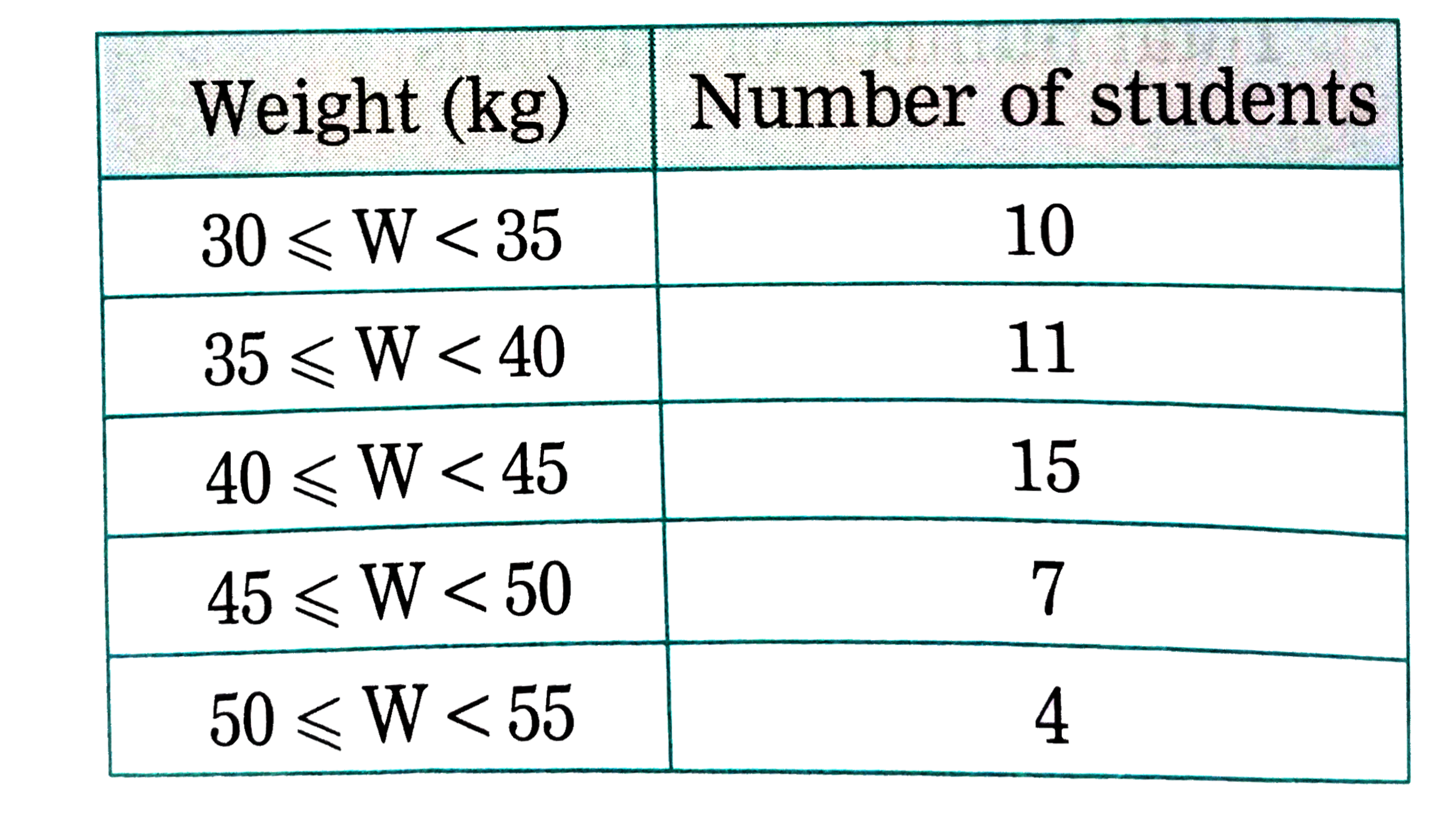
Find the median weight of a student.View SolutionFollowing table shows the weights of 12 students: Find the mean weight.
View SolutionFollowing frequency distribution gives the weights of 38 students of a class :
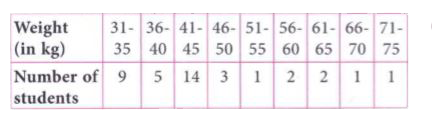
Based on the above information, answer the following questions.
Define an event whose probability is 1.View SolutionFollowing is the data showing weights of 40 students in a class . Find its median .
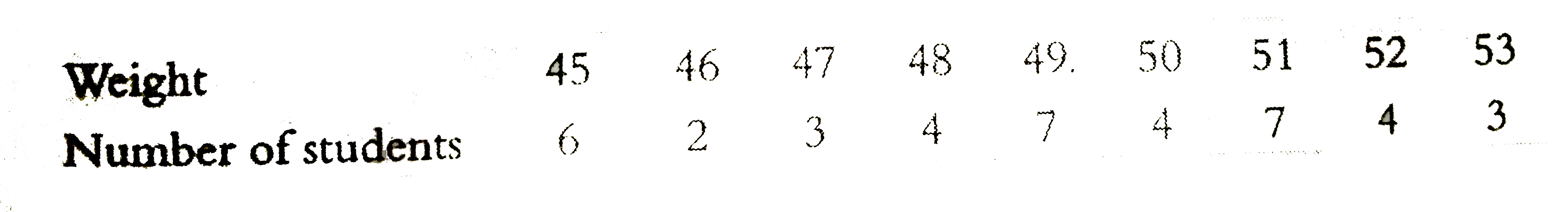 View Solution
View SolutionFind the mean weight of 20 students in your class.
View SolutionFollowing frequency distribution gives the weights of 40 students of a class .

A student from the class is chosen at random . What is the probability that the weight of the chosen student is
(i) at most 60 kg (ii) at least 56 kg (iii) not more than 50 kg ?View SolutionThe mean weight of 20 students is 25 kg and the mean weight of another 10 students in 40 kg . Find the mean weight of the 30 students .
View Solution

