In Fig. 10.59, AB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA . (FIGURE)
To solve the problem, we will follow these steps:
Step 1: Draw the Circle and Chord
- Draw a circle with center O and radius 10 cm.
- Draw chord AB such that the length of AB is 16 cm.
Hint: Remember that the radius is the distance from the center of the circle to any point on the circle.
Step 2: Identify the Midpoint of the Chord
- Let M be the midpoint of chord AB. Since AB = 16 cm, we have AM = MB = 8 cm.
Hint: The midpoint of a chord can be found by dividing the length of the chord by 2.
Step 3: Draw the Perpendicular from the Center to the Chord
- Draw a line from the center O to point M. This line OM is perpendicular to chord AB.
Hint: The perpendicular drawn from the center of a circle to a chord bisects the chord.
Step 4: Use the Pythagorean Theorem in Triangle OAM
- In triangle OAM, we have:
- OA = 10 cm (radius)
- AM = 8 cm (half the chord length)
- OM = ? (the distance from the center to the midpoint of the chord)
Using the Pythagorean theorem:
OA2=OM2+AM2
102=OM2+82
100=OM2+64
OM2=100−64=36
OM=6 cm
Hint: The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Step 5: Set Up the Right Triangle OAP
- Now consider triangle OAP where:
- OA = 10 cm (radius)
- OM = 6 cm (distance from center to midpoint)
- PM = ? (the distance from point P to point M)
Let PM = T. Then, by the Pythagorean theorem:
OA2=OP2+AP2
102=(T+6)2+AP2
Hint: Remember that the tangent at a point on a circle is perpendicular to the radius at that point.
Step 6: Set Up the Right Triangle PAM
- In triangle PAM, we have:
PA2=AM2+PM2
PA2=82+T2
PA2=64+T2
Hint: Again, apply the Pythagorean theorem to find the relationship between the sides of the triangle.
Step 7: Substitute and Solve
- Now we have two equations:
1. 100=(T+6)2+PA2
2. PA2=64+T2
Substituting the second equation into the first:
100=(T+6)2+(64+T2)
Expanding:
100=T2+12T+36+64+T2
Combining like terms:
100=2T2+12T+100
Subtract 100 from both sides:
0=2T2+12T
Factoring out:
0=2T(T+6)
Thus, T = 0 or T = -6 (not possible since distance cannot be negative).
Hint: When solving quadratic equations, factorization can simplify the process.
Step 8: Find PA
- Now substitute T = 0 back into the equation for PA:
PA2=64+02
PA2=64
PA=8 cm
Hint: To find the length, take the square root of the squared value.
Final Answer
The length of PA is 8 cm.
---
- Draw a circle with center O and radius 10 cm.
- Draw chord AB such that the length of AB is 16 cm.
- Let M be the midpoint of chord AB. Since AB = 16 cm, we have AM = MB = 8 cm.
- Draw a line from the center O to point M. This line OM is perpendicular to chord AB.
- In triangle OAM, we have:
- OA = 10 cm (radius)
- AM = 8 cm (half the chord length)
- OM = ? (the distance from the center to the midpoint of the chord)
OA2=OM2+AM2
102=OM2+82
100=OM2+64
OM2=100−64=36
OM=6 cm
- Now consider triangle OAP where:
- OA = 10 cm (radius)
- OM = 6 cm (distance from center to midpoint)
- PM = ? (the distance from point P to point M)
OA2=OP2+AP2
102=(T+6)2+AP2
- In triangle PAM, we have:
PA2=AM2+PM2
PA2=82+T2
PA2=64+T2
- Now we have two equations:
1. 100=(T+6)2+PA2
2. PA2=64+T2
100=(T+6)2+(64+T2)
Expanding:
100=T2+12T+36+64+T2
Combining like terms:
100=2T2+12T+100
Subtract 100 from both sides:
0=2T2+12T
Factoring out:
0=2T(T+6)
Thus, T = 0 or T = -6 (not possible since distance cannot be negative).
- Now substitute T = 0 back into the equation for PA:
PA2=64+02
PA2=64
PA=8 cm
The length of PA is 8 cm.
Topper's Solved these Questions
Similar Questions
In Fig. 10.59, AB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA . (FIGURE)
View SolutionAB is a chord of length 24cm of a circle of radius 13cm .The tangents at A and B intersect at a point C. Find the length AC
View Solution
Knowledge Check
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cm
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionIn Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
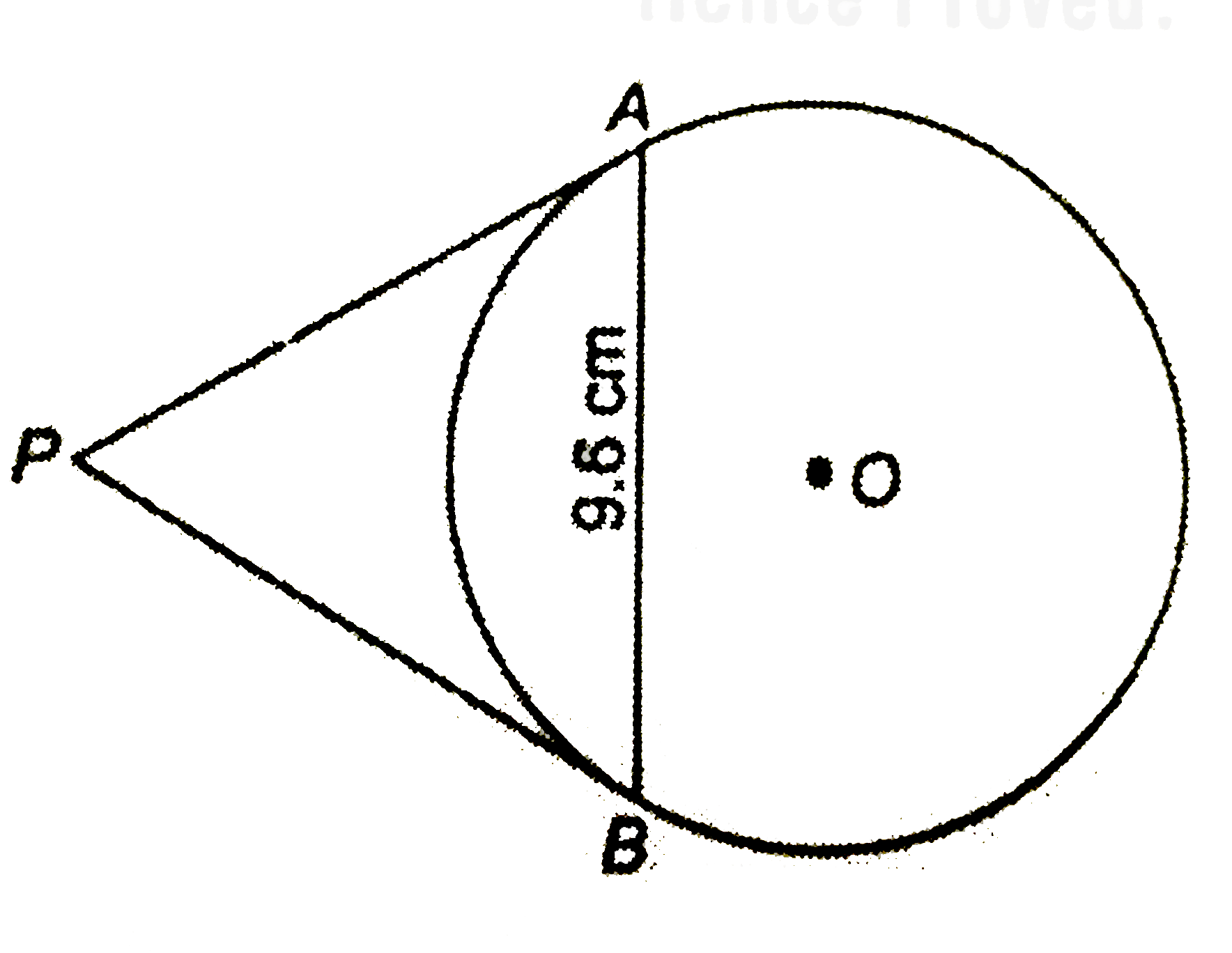
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionA chord AB of length 16 cm is drawn in a circle of diameter 20 cm. If tangents at A and B intersect each other at point P, find the length of PA.
View Solution
