Question

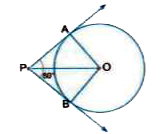
If tangents
$PA$
and $PB$
from a
point $P$
to a circle
with centre $O$
are
inclined to each other at an angle of $80o$
then $\angle POA$
is equal to
$50o$
(b) $60o$
(c) $70o$
(d) $80o$

Explanation

To solve the problem, we need to find the angle $$\angle POA$$ given that the tangents $$PA$$ and $$PB$$ from point $$P$$ to the circle are inclined to each other at an angle of $${80}^{\circ }$$.

1. Understand the Configuration:
- We have a circle with center \( O \).
- Tangents \( PA \) and \( PB \) touch the circle at points \( A \) and \( B \) respectively.
- The angle between the two tangents \( PA \) and \( PB \) is given as \( 80^\circ \).

2. Draw the Diagram:
- Draw the circle with center \( O \).
- Mark points \( A \) and \( B \) where the tangents touch the circle.
- Draw the tangents \( PA \) and \( PB \).
- Mark the angle \( \angle APB = 80^\circ \).

3. Identify the Angles:
- Since \( OA \) and \( OB \) are radii of the circle, the angles \( OAP \) and \( OBP \) are right angles (i.e., \( 90^\circ \)).
- Therefore, we can consider the quadrilateral \( OAPB \).

4. Calculate the Angle \( AOB \):
- The sum of the angles in quadrilateral \( OAPB \) is \( 360^\circ \).
- We know:
- \( \angle APB = 80^\circ \)
- \( \angle OAP = 90^\circ \)
- \( \angle OBP = 90^\circ \)
- Let \( \angle AOB = x \).
- Thus, we have:
\( 80^\circ + 90^\circ + 90^\circ + x = 360^\circ \)
- Simplifying gives:
\( 260^\circ + x = 360^\circ \implies x = 100^\circ \)
- Therefore, \( \angle AOB = 100^\circ \).

5. Consider Triangle \( OAB \):
- In triangle \( OAB \), since \( OA = OB \) (both are radii), the triangle is isosceles.
- Let \( \angle OAB = \angle OBA = \theta \).
- The sum of angles in triangle \( OAB \) is \( 180^\circ \):
\( \theta + \theta + 100^\circ = 180^\circ \)
- This simplifies to:
\( 2\theta + 100^\circ = 180^\circ \implies 2\theta = 80^\circ \implies \theta = 40^\circ \)
- Thus, \( \angle OAB = \angle OBA = 40^\circ \).

6. Find Angle \( POA \):
- Now consider triangle \( OAP \).
- We know:
- \( \angle OAP = 90^\circ \)
- \( \angle OAB = 40^\circ \)
- Let \( \angle POA = \phi \).
- The sum of angles in triangle \( OAP \) gives:
\( \phi + 40^\circ + 90^\circ = 180^\circ \)
- This simplifies to:
\( \phi + 130^\circ = 180^\circ \implies \phi = 50^\circ \)

Final Answer:
Thus, \( \angle POA = 50^\circ \).