Construct a triangle similar to a given ABC such that each of its sides is (5/7)th of the corresponding sides of ABC . It is given that AB=5cm , BC=7cm and ∠ABC=50o
To construct a triangle similar to triangle ABC such that each of its sides is 57 of the corresponding sides of triangle ABC, follow these steps:
1. Draw Triangle ABC:
- Start by drawing a line segment BC of length 7 cm. Mark the endpoints as B and C.
- Using a protractor, construct an angle of 50 degrees at point B.
- With a compass, measure 5 cm and mark this length from point B along the line forming the 50-degree angle. Label this point as A.
- You now have triangle ABC with sides AB = 5 cm, BC = 7 cm, and angle ABC = 50°.
2. Extend Line BC:
- Extend the line segment BC a little beyond point C to facilitate the construction of the similar triangle.
3. Construct an Acute Angle:
- At point B, draw an acute angle (you can choose any angle, but it should be less than 90 degrees) to help in dividing the angle for the ratio.
4. Divide the Angle into 7 Equal Parts:
- Using a compass, keep the same width and mark 7 equal arcs along the angle you just drew. Label these points as B1, B2, B3, B4, B5, B6, and B7.
5. Select the 5th Division:
- From point B, draw a line to point B5 (the 5th division). This line will represent the corresponding side of the smaller triangle.
6. Draw Parallel Lines:
- Now, using a compass, draw an arc from point B5. Without changing the compass width, draw an arc from point B7.
- Measure the angle from point B3 to B5 and extend this line to create a parallel line to BC. This will intersect the arc drawn from B5.
7. Repeat for Point C:
- Now repeat the process for point C. Draw an arc from point C and then, without changing the compass width, draw an arc from point B7.
- Measure the angle from point B3 to C and extend this line to create a parallel line to AB. This will intersect the arc drawn from C.
8. Label the New Points:
- The intersection points of the parallel lines with the arcs will give you points A' and C'. Label these points accordingly.
9. Final Triangle:
- Connect points A', B, and C' to form triangle A'BC'. This triangle is similar to triangle ABC, with each side being 57 of the corresponding sides of triangle ABC.
- Start by drawing a line segment BC of length 7 cm. Mark the endpoints as B and C.
- Using a protractor, construct an angle of 50 degrees at point B.
- With a compass, measure 5 cm and mark this length from point B along the line forming the 50-degree angle. Label this point as A.
- You now have triangle ABC with sides AB = 5 cm, BC = 7 cm, and angle ABC = 50°.
- Extend the line segment BC a little beyond point C to facilitate the construction of the similar triangle.
- At point B, draw an acute angle (you can choose any angle, but it should be less than 90 degrees) to help in dividing the angle for the ratio.
- Using a compass, keep the same width and mark 7 equal arcs along the angle you just drew. Label these points as B1, B2, B3, B4, B5, B6, and B7.
- From point B, draw a line to point B5 (the 5th division). This line will represent the corresponding side of the smaller triangle.
- Now, using a compass, draw an arc from point B5. Without changing the compass width, draw an arc from point B7.
- Measure the angle from point B3 to B5 and extend this line to create a parallel line to BC. This will intersect the arc drawn from B5.
- Now repeat the process for point C. Draw an arc from point C and then, without changing the compass width, draw an arc from point B7.
- Measure the angle from point B3 to C and extend this line to create a parallel line to AB. This will intersect the arc drawn from C.
- The intersection points of the parallel lines with the arcs will give you points A' and C'. Label these points accordingly.
- Connect points A', B, and C' to form triangle A'BC'. This triangle is similar to triangle ABC, with each side being 57 of the corresponding sides of triangle ABC.
Topper's Solved these Questions
Similar Questions
To constuct a triangle similar to a given ΔABC with its sides 73 of the corresponding side of ΔABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect of BC. The points B1,B2,…..,B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C, where C' lines on BC produced. Finally line segment A'C' is drawn parallel to AC.
View SolutionDraw ΔABC with sides = 6 cm, 8 cm and 9 cm and then construct a triangle similar to ΔA'B'C whose sides are 35 or the corresponding sides of ΔABC.
View Solution
Knowledge Check
If sides of triangle ABC are a, b, and c such that 2b=a+c, then
Abc>23Bbc>13Cbc<2Dbc<32In a ΔABC,a,b,A are given and c1,c2 are two valus of the third side c. The sum of the areas two triangles with sides a,b,c1anda,b,c2 is
A12a2sin2AB12b2sin2ACb2sin2ADa2sin2A
Draw a triangle ABC with BC=7cm, ∠B=450and∠C=600. Then construct another triangle, whose sides are 35 times the corresponding sides of triangle ABC.
View SolutionThe area of a triangle is half the product of any of its sides and the corresponding altitude. GIVEN : A ABC in which AL is the altitude to the side BC. TO PROVE : ar(ABC)=12(BC×AL) CONSTRUCTION : Through C and A draw CDBA and ADBC respectively, intersecting each other at D.
View SolutionP and Q are points on sides AB and AC respectively of ABC . If AP=3cm , PB=6cm , AQ=5cm and QC=10cm , show that BC=3 PQ .
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
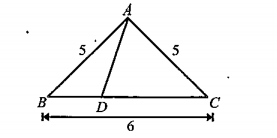
View SolutionFigure shows triangle ABC such that AB=AC=5,BC=6.P∮DisonB Csuchtˆ(B D)/(D C)=1/2,then□of≤n>hofsA D is
View SolutionIf A:B=5:6 and B:C=4:7 find A:B:C
View Solution
