In the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
Step by step video & image solution for In the Fig. 13.12, J K L M is a square with sides of length 6 units. Points A and B are the mid-points of sides K L and L M respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of J A B ? (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionA point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is
View Solution
Knowledge Check
L and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
 AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of theseLet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NMOPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionIn A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
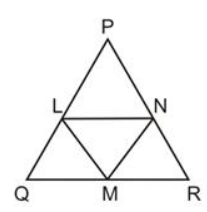
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionOPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
View SolutionPQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
View Solution
