In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
Here, Side of the squareABCD=2∗1=2 units
∴ Area of square ABCD(A1)=22=4 square units
Now, area of the shaded region (AS)=A1−4∗πr24
⇒AS=4−π(1)2=4−π
So, the required probability =ASA1=4−π4=1−π4.
Similar Questions
In figure, a dart is thrown and lands n the interior of the circle. What is the probability that the dart will land in the shaded region?
View SolutionIn figure, a dart is thrown and lands in the interior of the circle. What is the probability that the dart will land in the shaded region?
View Solution
Knowledge Check
A point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is
A34B14C12D23

In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in the shaded region ?
View SolutionIn the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionIn the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionIn the adjoining figure a dart is thrown at the dart board and lands in the interior of the circle . What is the probability that the dart will land in the shaded region.
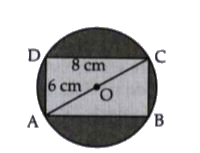
View SolutionA point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is
View Solution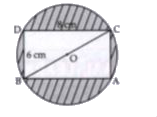
In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in rectangle ABCD region ?
View Solution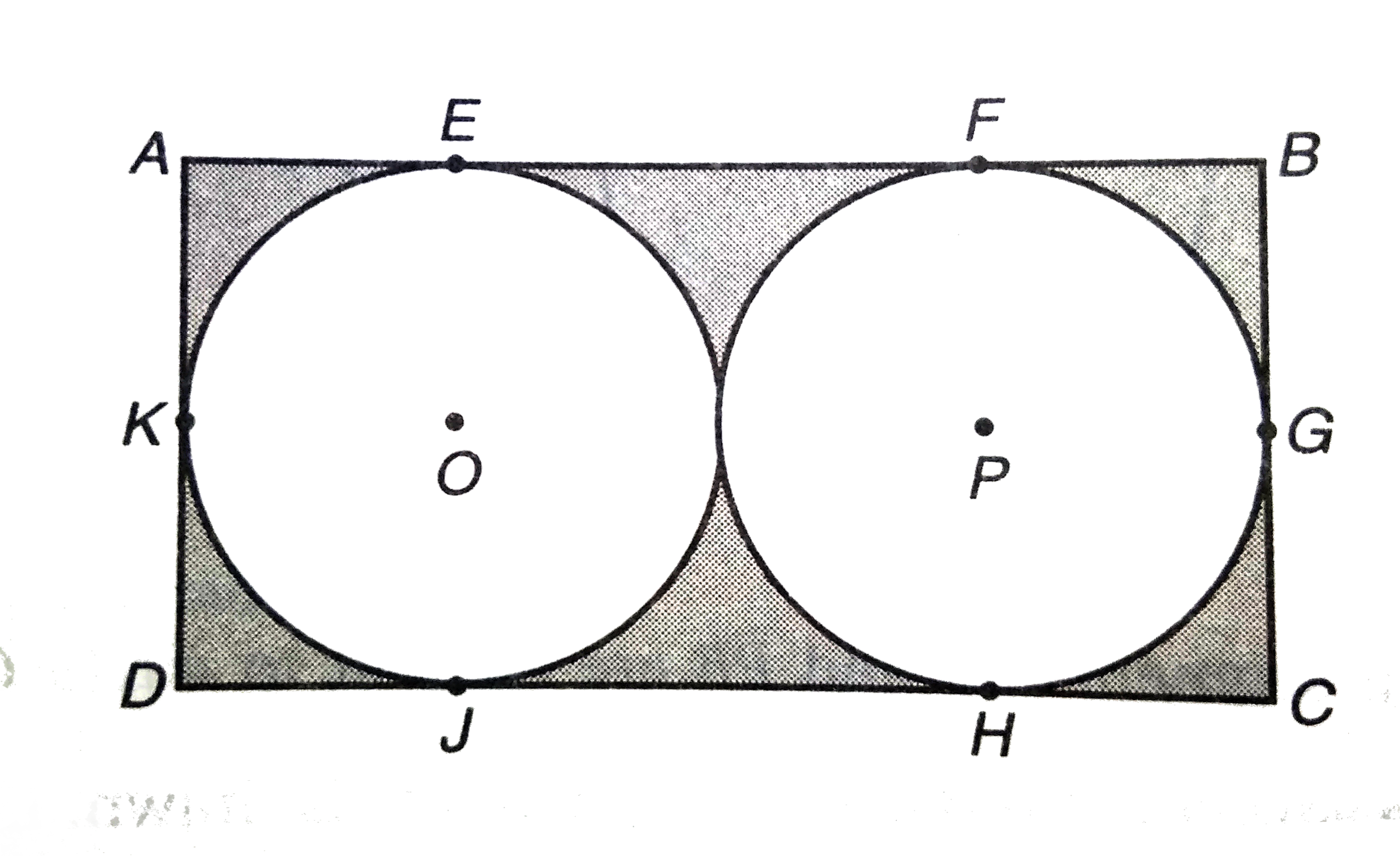
In the figure above, the radius of each circle is 1. If circles O and P touch the sides of rectangle ABCD only at the lettered points, what is the area of the shaded region?
View Solution
