In two triangles ABC and DEF, it is given that ∠A=∠D, ∠B=∠E and ∠C=∠F. Are the two triangles necessarily congruent?
Solution
No.
Reason: Two triangles are not necessarily congruent, because we know only angle angle-angle '(AAA)' criterion. This criterion can produce similar but not congruent triangles.
Topper's Solved these Questions
Similar Questions
In two triangles ABC and DEF, it is given that ∠A=∠D, ∠B=∠E and ∠C=∠F. Are the two triangles necessarily congruent?
View SolutionTwo triangles ABC and DEF such that ∠A=∠D,∠B=∠Eand∠C=∠F. Then
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionIf in two triangles ABC and DEF , ∠A=∠E, ∠B=∠F , then which of the following is not true? BCDF=ACDE (b) ABDE=BCDF (c) ABEF=ACDE (d) BCDF=ABEF
View Solution∠A+∠B+∠C+∠D+∠E=
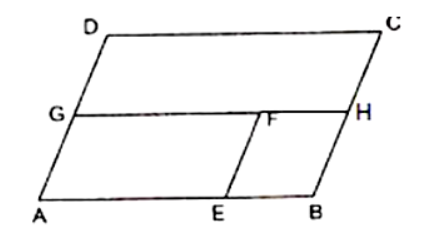
View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
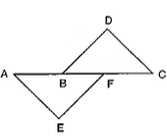
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
View Solution