In two triangles ABC and ADC, if AB=AD and BC=CD. Are they congruent?
Solution
The given triangles will be congruent by the 'SSS' congruency.
'AB=AD' (Given)
'BC=CD' (Given)
Thus, according to the figure which will be formed -
In △ABC and △ADC
'AB = AD' (Given)
'BC = CD' (Given)
'AC= AC' (Common Side) -
Therefore, By the side side side '(SSS)' congruency -
△ABC=△ADC
Hence Proved
Topper's Solved these Questions
Similar Questions
Fill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
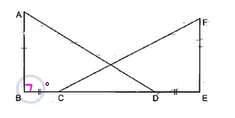
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
 View Solution
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn a parallelogram ABCD , write the sum of angle A and B
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
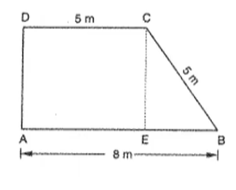
View SolutionIn quadrilateral ABCD show in Figure. ABDC and AD⊥AB. Also, AB=8m, DC=BC=5m. Find the area of the quadrilateral.
 View Solution
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View Solution

