In Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
"given PQRS
is a parallelogram, PO and QO are, respectively, the
angle bisectors of ∠P and ∠Q
Line LOM is drawn parallel to PQ
(i)PL=QM
so in PQML ,PQ∣∣LMand PL∣∣QM, so it is a parallelogram
so
PL=QM
(ii)
LO=OM
in figure traingle PLO and QMO,
∠LPO=∠MQO and ∠QOM=∠OQM
so PL=LO....(1) and
QM=MO.....(2)
(in isosceles traingle side opposite to equal angles are equal)
and PQRS is also a parallelogram so PL=QM....(3)
from 1,2,3 we have LO=OM"
Topper's Solved these Questions
Similar Questions
PQRS is a parallelogram. PXandQY are respectively, the perpendiculars from PandQ to SRandRS produced. Prove that PX=QY
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
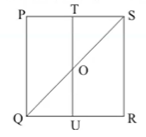 View Solution
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
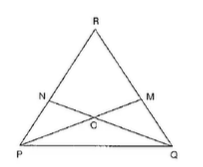 View Solution
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
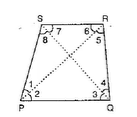 View Solution
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
 View Solution
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View Solution

