PQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
As we know that if a triangle and a parallelogram are on the same base and between the same parallels, the area of triangle is equal to half area of parallelogram.
Area (△ABP) = Area (△ASB) ______1
Area (△ARQ) = Area (△ARB) ____2
Now, Area(△ASR)=area(△ASB)+area(△ARB)
area(△ABP)=area(△ARQ)
area(△PBQ)
=17cm2
Hence, area of (△ASR) is 17cm2.
Topper's Solved these Questions
Similar Questions
PQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View Solution
Knowledge Check
- Question 1 - Select One
If p,q,r and s are positive real numbers such that p+q+r+s=2, then M=(p+q)(r+s) satisfies the relation, when (A) 0<M≤1 (B) 1≤M≤2 .(C) 2≤M≤3 (D) 3≤M≤4
A0<M≤1B1≤M≤2C2≤M≤3D3≤M≤4 - Question 2 - Select One
If P is the husband of Q and R is the mother of S and Q, what is R to P?
A(a) MotherB(b) SisterC(c) AuntD(d) Mother-in-law
In ABC , P divides the side AB such that AP:PB=1:2 . Q is a point in AC such that PQBC . Find the ratio of the areas of APQ and trapezium BPQC .
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
 View Solution
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
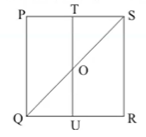 View Solution
View Solution

