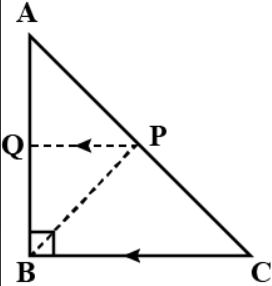
ABC
is a triangle right
angled at B;and P
is the mid-point of AC
. Prove that:
PQ ⊥AB
(ii)
Q
is the mid point of AB (iii)
PB=PA=12AC
Step by step video & image solution for A B C is a triangle right angled at B ; a n d\ P is the mid-point of A C . Prove that: P Q\ _|_A B (ii) Q is the mid point of A B (iii) P B=P A=1/2A C by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD⊥AC
(iii) CM = MA=12AB
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionABC is a triangle, P is a point on ABandQ is a point on AC such that ∠AQP=∠ABC. Complete the relation AreaofAPQAreaofABC=.()AC2 .
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View Solution
