Prove that
of all parallelograms of which the sides are given, the parallelogram which
is rectangle has the greatest area.
Video Solution
Text Solution
"Given: A parallelogram ABCD whose sides are given.
To prove: The area of the parallelogram ABCD is the greatest when it is a rectangle.
Cons.: Draw DE⊥AB.
Proof : Area of parallelogram ABCD = Base x corresponding altitude = AB×DE
When parallelogram ABCD is a rectangle, then its area is ABxxDA ( ∠DAB=90⋅)
In right △ DEA,
∠DEA>∠DAE
DA>DE
Sides opposite to greater angle of a triangle is longer
∴ ar(rectangle ABCD)>ar(parallelogram ABCD) i.e the area of the parallelogram ABCD is the greatest when it is a rectangle."
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which statement is true about all parallelogram
AThe diagonals are congruent.BThe area is the product of two adjacent sidesCThe opposite angles are congruentDThe diagonals are perpendicular to each other.
Prove that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionA rhombus is a parallelogram in which __________ sides are equal.
View SolutionIf the adjacent sides of a parallelogram are equal then parallelogram is a
View SolutionThe given figure shows a parallelogram of 20 m height. The base of the parallelogram is 40 m long.
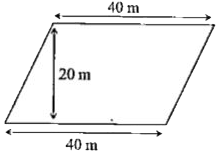
What is the area of the parallelogram?
View SolutionThe angle bisectors of a parallelogram form a rectangle.
View SolutionThe angle bisectors of a parallelogram form a rectangle.
View Solution