If ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
Solution:
ABCD is a parallelogram.
When we join the diagonal of parallelogram, it divides it into two quadrilaterals.
Step 1:
Let AC is the diagonal, then, Area(△ABC)=Area(△ACD)=12(Areaof| |gmABCD)
Step 2:
Let BD be another diagonal
Area(△ABD)=Area(△BCD)=12(Areaof| |gmABCD)
Now, From Step 1 and step 2, we have
Area(△ABC)=Area(△ACD)=Area(△ABD)=Area(△BCD)=12(Areaof| |gmABCD)
Hence Proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If △ABC - △PQR and BCQR = 14 then ar(△PQR)ar(△ABC) =
A14B41C116D161 - Question 2 - Select One
If ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
A√k21+k22+k23B√k1k2k3k21+k22+k23C√∣∣(k21+k22−k23)∣∣D√∣∣(k21−k22−k23)∣∣
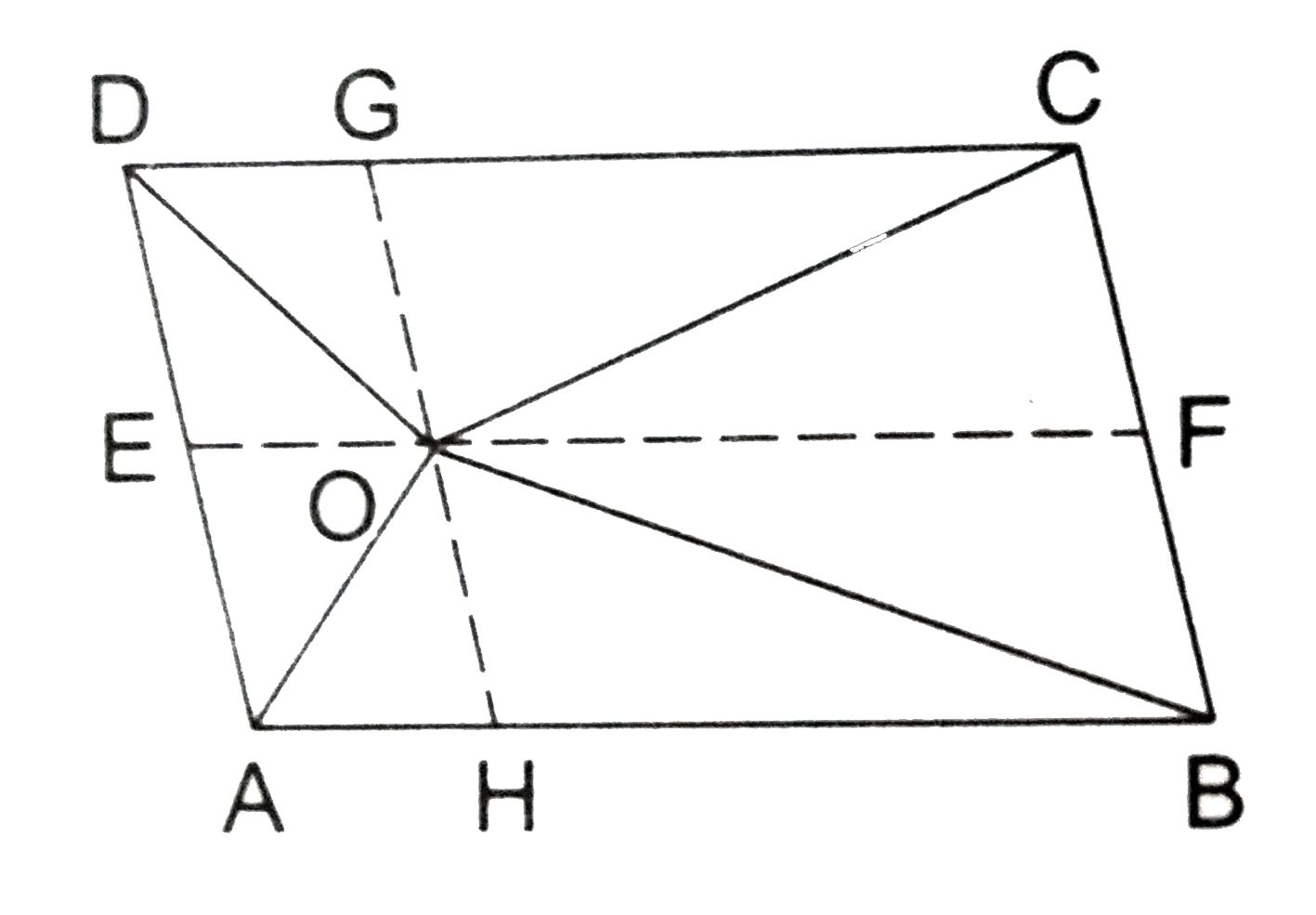
ABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
 View Solution
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
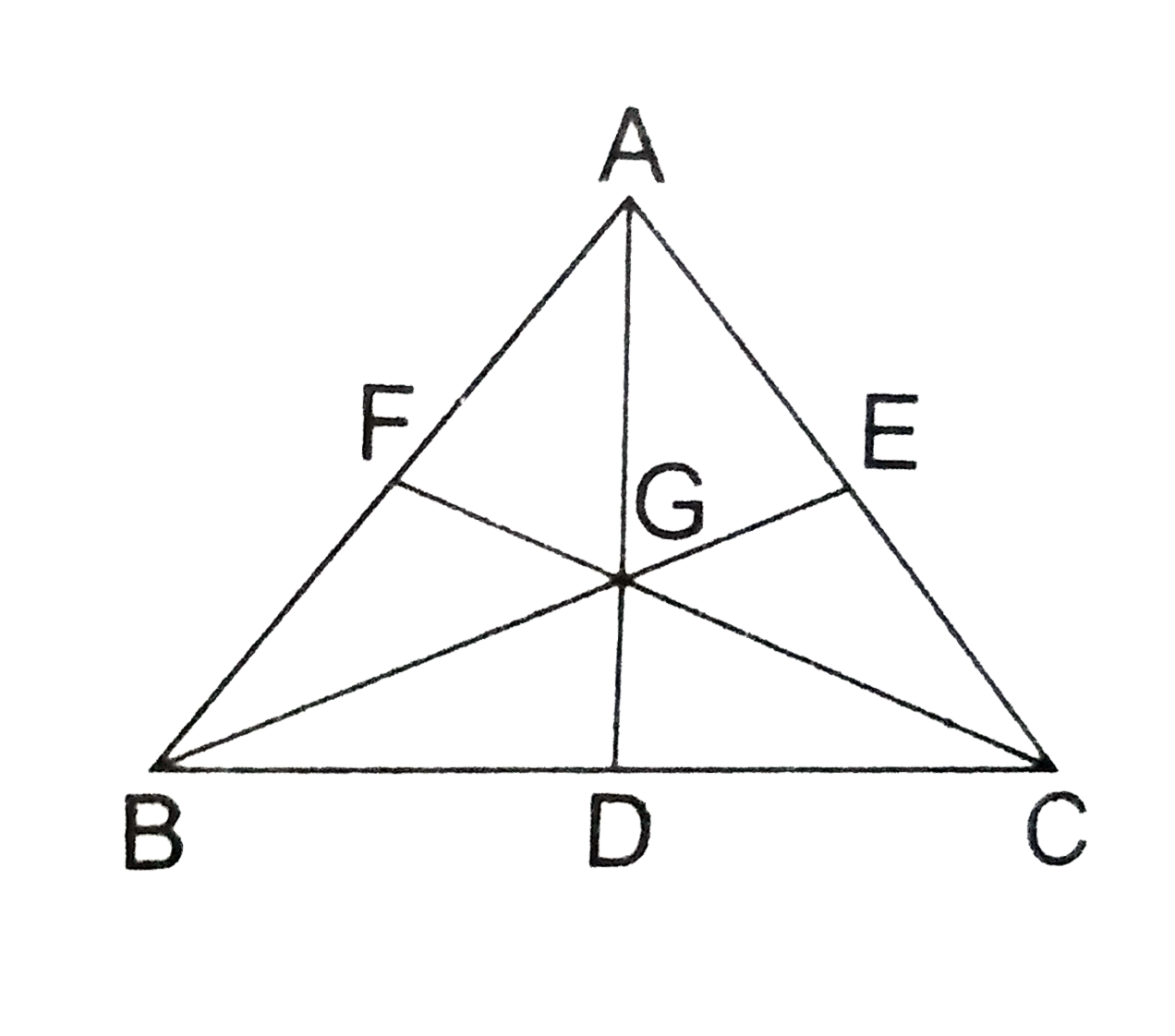
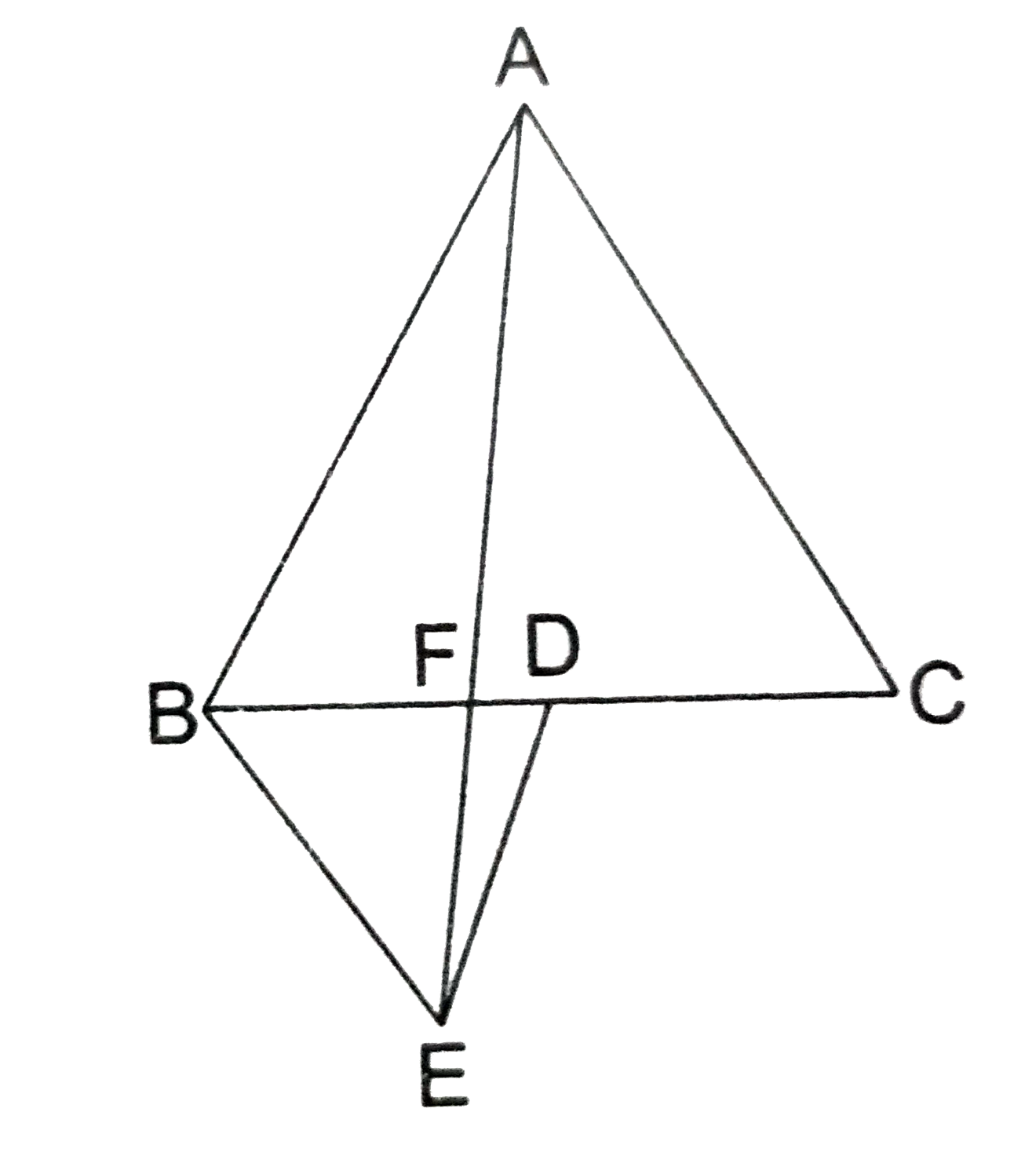
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
 View Solution
View Solution△ABC~△EDF and ar(△ABC):ar(△DEF)=1:4. If AB =7cm, BC = 8 cm and CA = 9 cm, then DF is equal to :
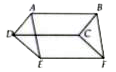
△ABC~△EDF और ar(△ABC):ar(△DEF)=1:4 है। यदि AB = 7 सेमी, BC = 8 सेमी तथा CA = 9 सेमी है, तो DF का मान किसके बराबर होगा?View SolutionIn the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
 View Solution
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View Solution