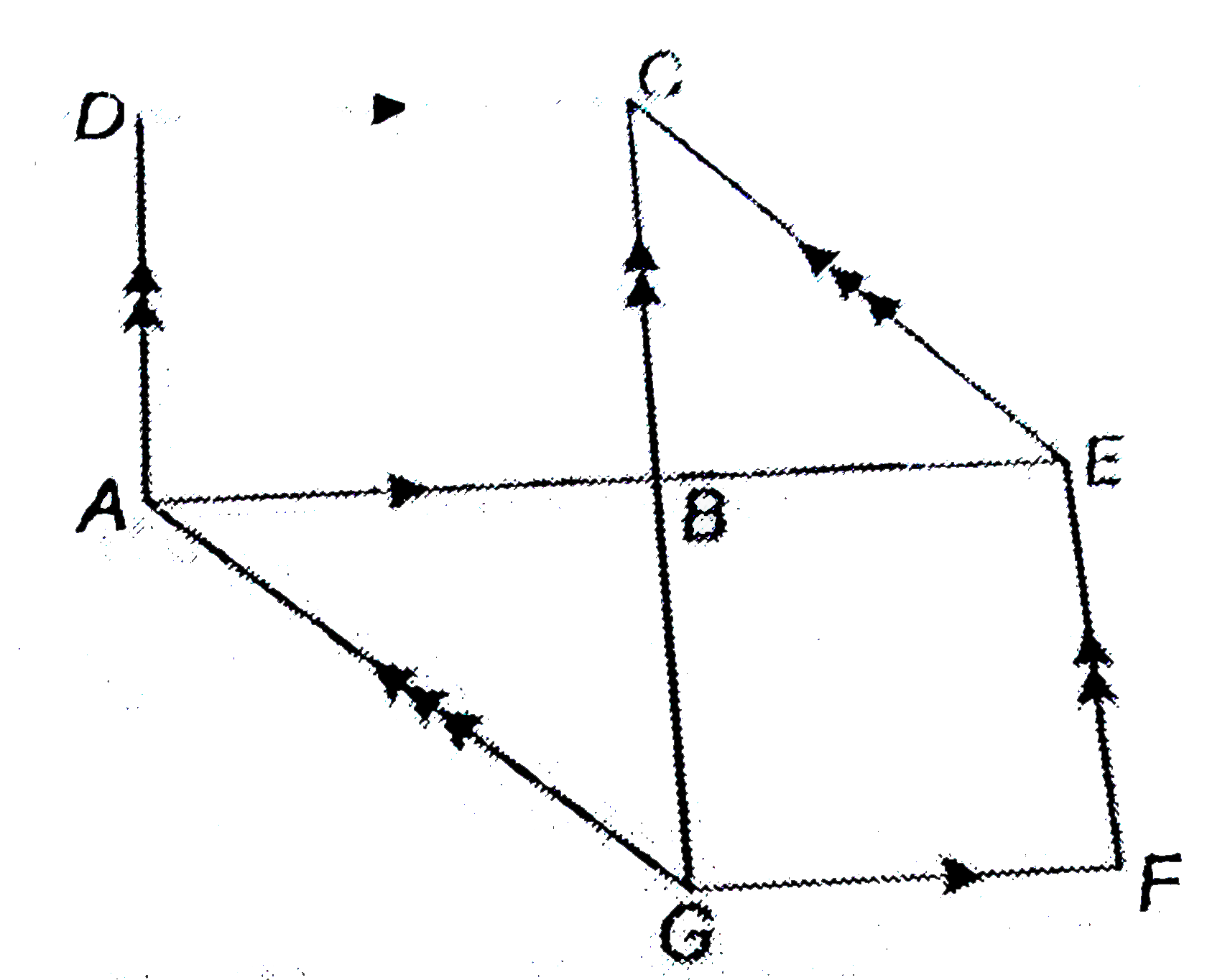
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
Solution
Construction
Let us join AC and PQ.
△ACQ and △AQP are on the same base AQ and are between same parallels AQ and CP.
∴Area(△ACQ)=Area(△APQ)
⇒Area(△ACQ)−Area(△ABQ)=Area(△ACQ)−Area(△ABQ)
⇒Area (△ABC)= Area (△ABQ)...(1)
Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively,
So,
Area (△ABC)=12 Area of parallelogram ABCD...(2)
Area (△QBP)=12 Area of parallelogram BPRQ...(3)
From equations (1),(2), and (3), we get
12Area of parallelogram ABCD=12 Area of parallelogram BPRQ
∴Area of parallelogram ABCD= Area of parallelogram BPRQ
Hence proved, areas of both parallelograms are equal.
Topper's Solved these Questions
Similar Questions
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).

View Solution
Knowledge Check
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of ||gmABCD= area of ||gmBEFG.
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
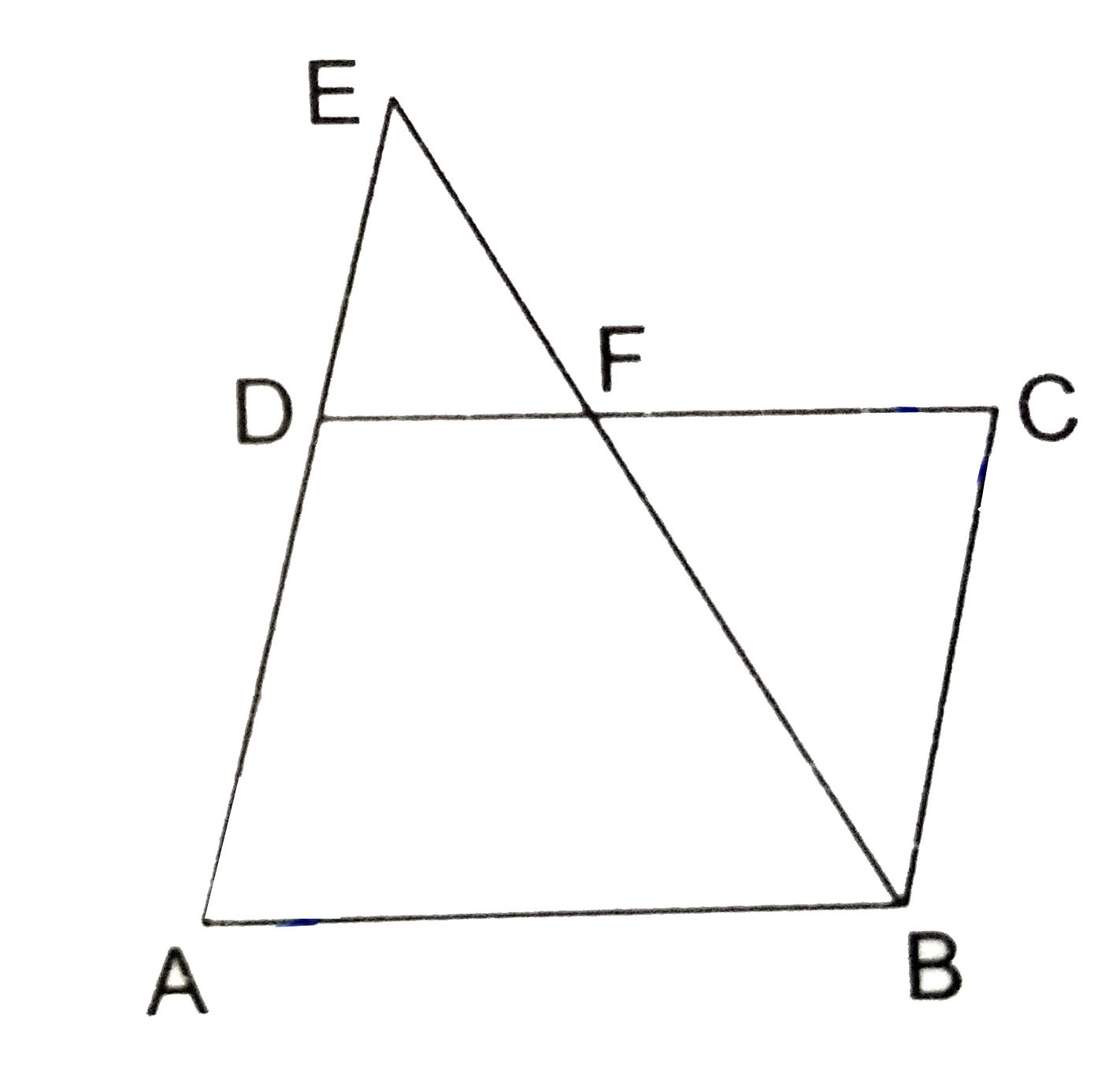
View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

ar(ΔAEDF) = ar(ΔABCDE)
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution
