D, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
Given: A ΔABC in which D,E,F are the mid-point of the side BC, CA and AB respectively. To prove: (i) Quadrilateral BDEF is parallelogram.
(ii) ar(║gm BDEF)=1/2ar(/_\ABC).
(iii) ar(△DEF)=14ar(△ABC). Proof: (i) In △ABC,
∴F is the mid-point of side AB and E is the midpoint of side AC.
∴EF║BD [∵Line joining the mid-points of any two sides of a triangle is parallel to the third side.]
Similarly, ED║FB.
Hence, BDEF is a parallelogram.
Hence Proved.
(ii) Similarly, prove that AFDE and FDCE are parallelograms.
∴FD is diagonals of parallelogram BDEF.
∴ar(△FBD)=ar(△DEF) ...(i)
Similarly, ar(△FAE)=ar(△DEF) . ..(ii)
And ar(△DCE)=ar(△DEF) ...(iii)
From equations (i), (ii) and (iii), we get:
ar(△FBD)=ar(△FAE)=ar(△DCE)=ar(△DEF)
And ar(△FBD)+ar(△DCE)+ar(△DEF)+ar(△FAE)=ar(△ABC)
⇒2[ar(△FBD)+ar(△DEF)]=ar(△ABC)
⇒2[ar(║gmBDEF)]=ar(△ABC)
⇒ar(║gmBDEF)=12ar(△ABC)
(iii) Since, △ABC is divided into four non-overlapping triangles FBD, FAE, DCE and DEF.
From (i), (ii) and (iii)
∴ar(△ABC)=ar(△FBD)+ar(△FAE)+ar(△DCE)+ar(△DEF)
⇒ar(△ABC)=4ar(△DEF)
⇒ar(△DEF)=12ar(△ABC).
Topper's Solved these Questions
Similar Questions
D, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogramView SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
 View Solution
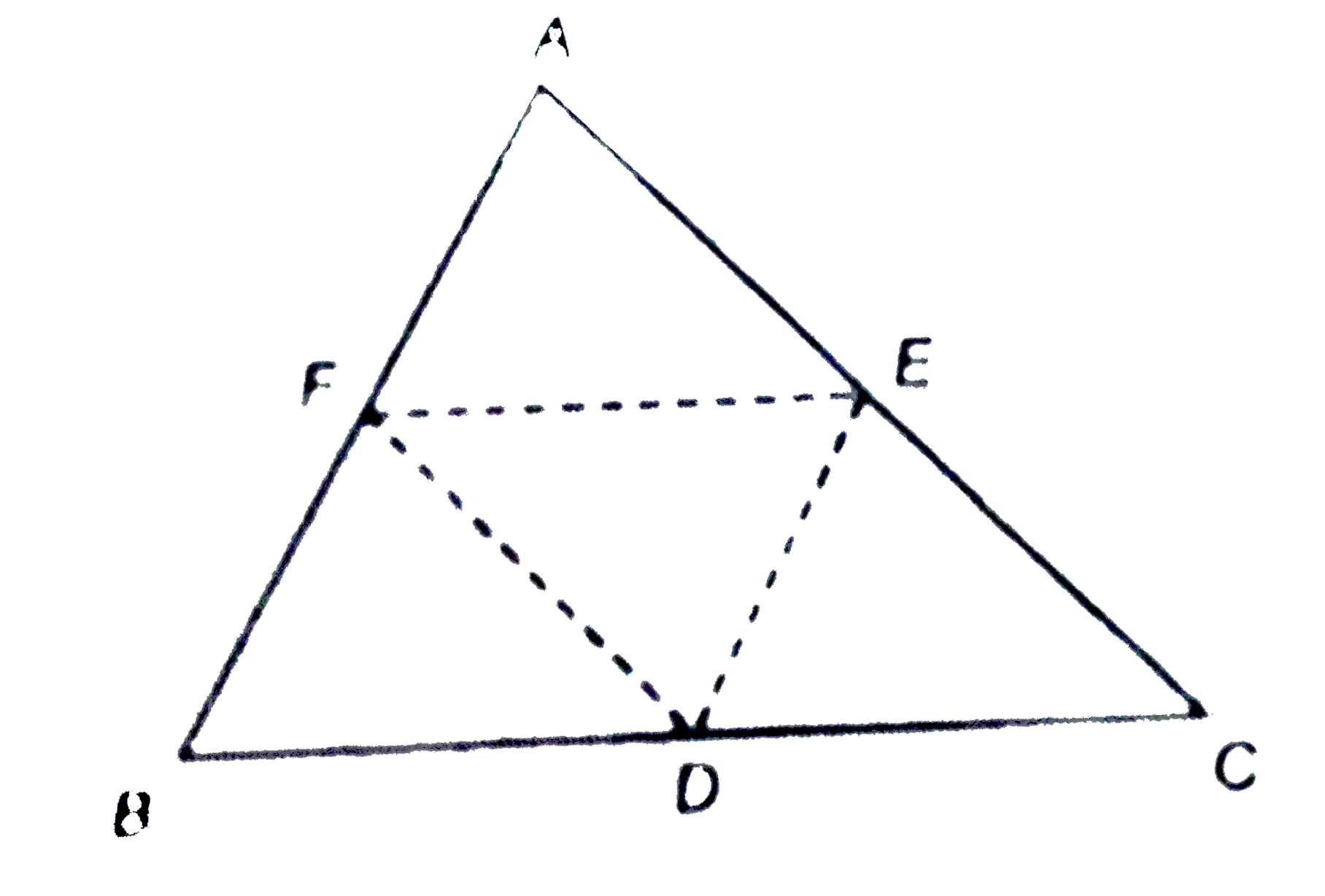
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC
 View Solution
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View Solution

