A force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
F1 most be equal to F2
F1 may be equal to F2
F1 must be unequal to F2
None of these
The correct Answer is:B
v2=0+F1ms1
0=v2−F2ms2
F1s1=F2s2
Topper's Solved these Questions
Similar Questions
A time dependent force F=3t^(2)+6t acts on a particle of mass 18kg .If particle starts from rest the work done by the force during the first 3 second will be :
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A 5kg. mass is accelerated from rest to 60 m/s in 1 sec. what force acts on it:-
A5×60NB(5/60)×981NC602×52ND(52)×602×981N - Question 2 - Select One
A time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
A9JB18JC4.5JD22J - Question 3 - Select One
When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
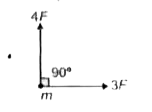 AaB2aC5aD8a
AaB2aC5aD8a
When a force F1 acts on a particle, frequency is 6 Hz and when a force F2 acts, frequency is 8 Hz. What is the frequency when both the forces act simultaneously in the same direction?
View SolutionGiven four forces : →F1=3ˆi−ˆj+9ˆk →F2=2ˆi−2ˆj+16ˆk →F3=9ˆi+ˆj+18ˆk →F4=ˆi+2ˆj−18ˆk If all these forces act on a particle at rest at the origin of a coordinate system, then identify the plane in which the particle would begin to move ?
View SolutionWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
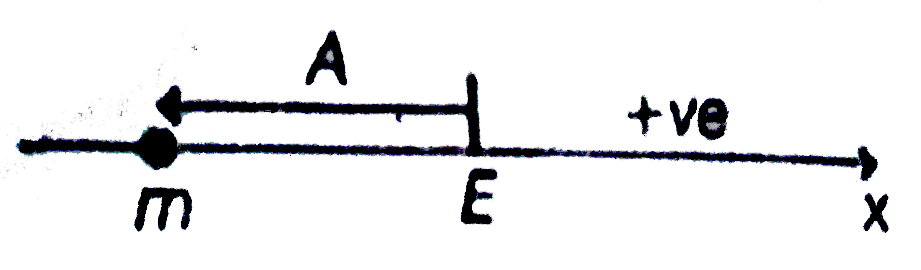 View Solution
View Solution

