At t=0 , switch S closed. Find the ratio of the rate at which magnetic energy stored in the coil to the rate at which energy is supplied by the battery at time t=τ=L/R .
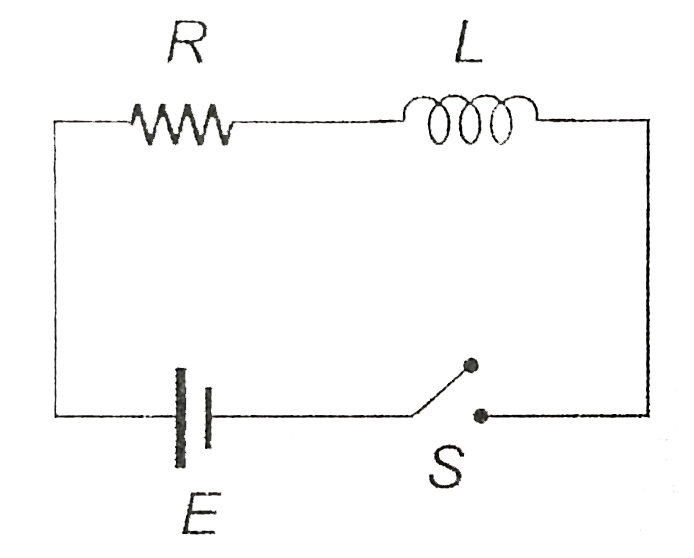
In R−L circuit, growth of current
i=i0(1−e−t/τ)
where i0=ER , τLR
didt=i0e−t/ττ
Magnetic energy stored in the coil
U=12Li2
αdUdt=12L.2ididt=Lididt
The rate at which energy supplied by battery
β=Ei
(α)(β)=L/dtEi=LEdidt
LE.i0e−t/ττ
At t=τ
αβ=LEi0e−1τ=LE.ER.RL.e
1e
Topper's Solved these Questions
Similar Questions
A coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionA3 H inductor is placed in series with 10Ω resistor and an emf of 10V is applied to the combination. Find
(i) the current at 0.3s,
(ii) the rate of increase of current at 0.3s,
(iii) the rate at which energy is dissipated as heat at t=0.3s.
(iv) the rate at which energy is stored in the magnetic field at 0.3s.
(v) the rate at which energy is delivered by the battery, and
(vi) the energy stored when the current has attained steady value.
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
View SolutionAt t=0 , switch S is closed. Find time constant of the circuit and current through inductor as a function of time t .

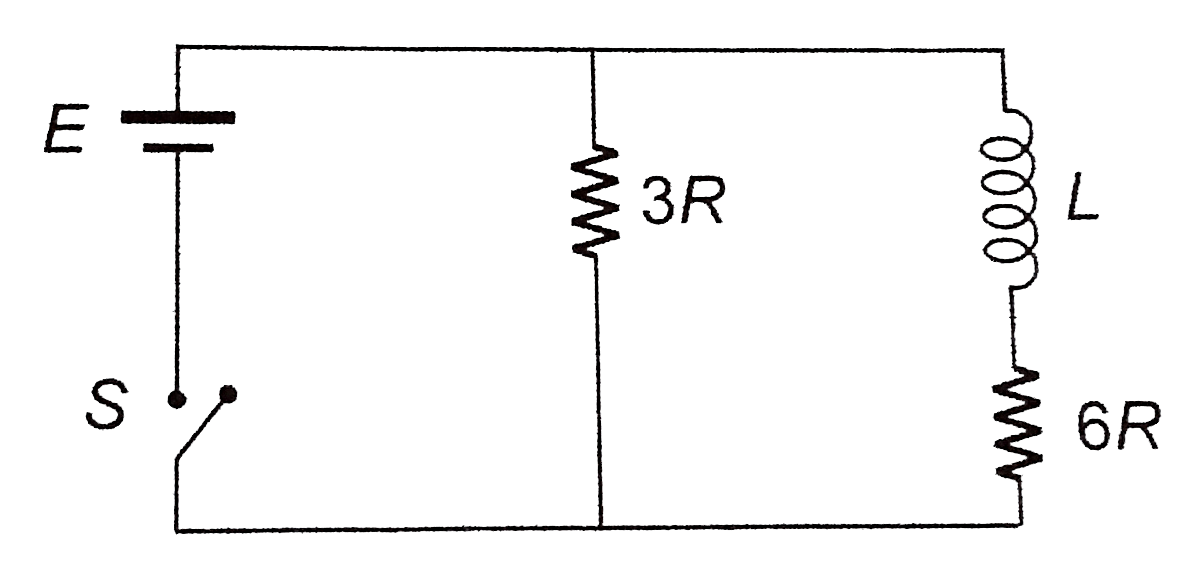
View SolutionIn steady state, calculate energy stored in capacitors shown in Fig. and the rate at which battery supplies energy

View SolutionA coil of reistance 5Ω and inductance 1H is connected to a battery of 10V. At t=0s, calculate (i) the current in the circuit (ii) the rate of rise of current (iii) the rate at which energy is supplied by the battery, (iv) the rate at which energy is dissipated as heat and (v) the rate at which energy is stored in the magnetic field of the coil.
View Solution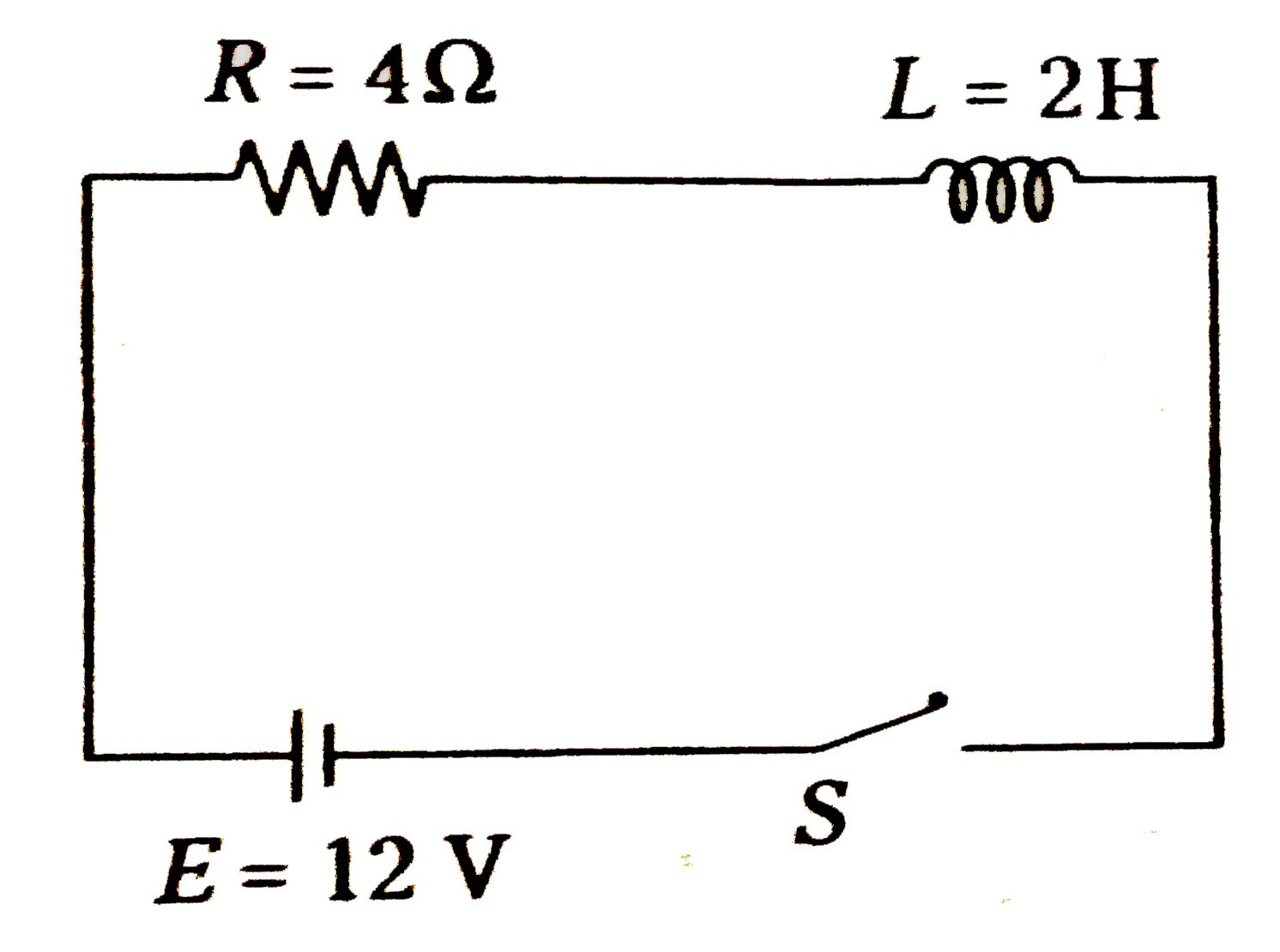
At t = 0, switch S is closed, calculate
(i) initial rate of increase of current, i.e., didtat t=0.
(ii) didt at time when current in the circuit is 0.5A.
(iii) Current at t = 0.6 s.
(iv) rate at which energy of magnetic field is increasing, rate of heat produced in resistance and rate at which energy is supplied by battery when i = 0.5 A.
(v) energy stored in inductor in steady state.
View SolutionAt t=0 , switch S is closed, calculate
(a) initial rate of increase of current i.e. didt at t=0
(b) didt at time when current in the circiut is 1A
(c) current at t=0.5sec
(d) rate at which energy of magnetic field is incresing, rate of heat produced in resistance and rate at which energy is supplied by battery when i=1A
(e) energy stored in inductor in steady state
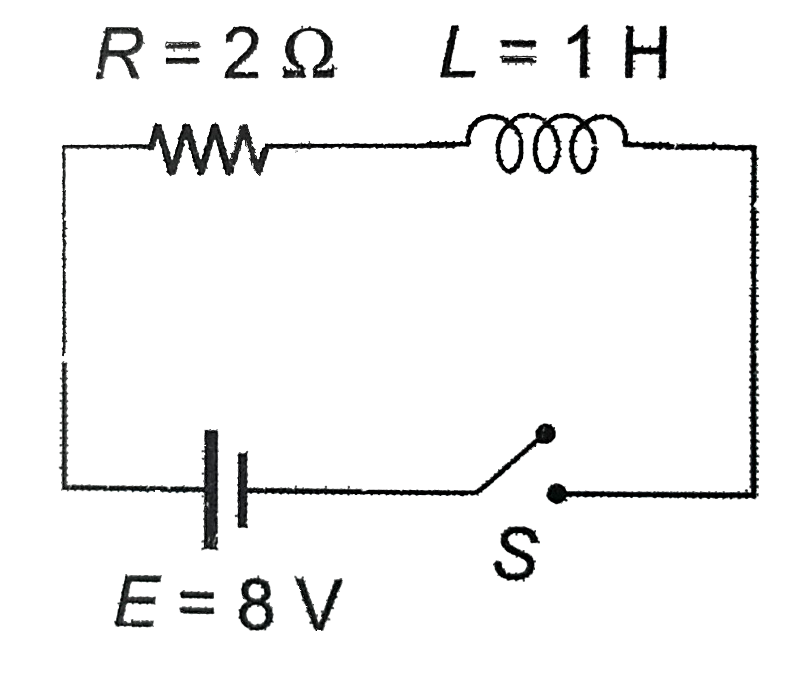
View SolutionIf a battery of emf E, internal resistance r is being charged by a current Ifrom a charge then the rate at which energy is supplied by charger is ……. And the rate at which chemical energy is stored in the battery is ……
View SolutionThe switch is closed at t=0. The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) ln2 (B) 12ln2 (C) 14ln2 (D) 2ln2
View Solution