The switch is closed at t=0. The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) ln2 (B) 12ln2 (C) 14ln2 (D) 2ln2
To solve the problem, we need to find the time t after which the rate of energy dissipation in the resistor is equal to the rate of energy storage in the inductor in an LR circuit.
1. Understand the Circuit: We have an LR circuit with a resistor R and an inductor L. When the switch is closed at t=0, a current I(t) starts to flow through the circuit.
2. Current in the Circuit: The current I(t) in the circuit can be expressed as:
I(t)=ER(1−e−RLt)
where E is the EMF of the battery.
3. Rate of Energy Dissipation in the Resistor: The power (rate of energy dissipation) in the resistor is given by:
PR=I2R
Substituting the expression for I(t):
PR=(ER(1−e−RLt))2R=E2R(1−e−RLt)2
4. Rate of Energy Storage in the Inductor: The power (rate of energy storage) in the inductor is given by:
PL=LdIdt
We need to find dIdt:
dIdt=ELe−RLt
Therefore,
PL=L⋅ELe−RLt=Ee−RLt
5. Set the Powers Equal: We want to find the time t when PR=PL:
E2R(1−e−RLt)2=Ee−RLt
6. Simplify the Equation: Dividing both sides by E (assuming E≠0):
ER(1−e−RLt)2=e−RLt
7. Let x=e−RLt: Then, we can rewrite the equation:
ER(1−x)2=x
8. Rearranging: Expanding and rearranging gives:
ER(1−2x+x2)=x
ER−(2ER+1)x+ERx2=0
9. Solve the Quadratic Equation: This is a quadratic equation in x. Using the quadratic formula:
x=−b±√b2−4ac2a
where a=ER,b=−(2ER+1),c=−ER.
10. Find t: Once we find x, we can find t using:
t=−LRlnx
11. Final Calculation: After solving for t, we find that:
t=LRln2
12. Substituting τ=LR gives us:
t=τln2
Thus, the time after which the rate of dissipation of energy in the resistor is equal to the rate at which energy is being stored in the inductor is:
t=τln2
where τ=LR.
Answer:
The correct option is (A) ln2.
I(t)=ER(1−e−RLt)
where E is the EMF of the battery.
PR=I2R
Substituting the expression for I(t):
PR=(ER(1−e−RLt))2R=E2R(1−e−RLt)2
PL=LdIdt
We need to find dIdt:
dIdt=ELe−RLt
Therefore,
PL=L⋅ELe−RLt=Ee−RLt
E2R(1−e−RLt)2=Ee−RLt
ER(1−e−RLt)2=e−RLt
ER(1−x)2=x
ER(1−2x+x2)=x
ER−(2ER+1)x+ERx2=0
x=−b±√b2−4ac2a
where a=ER,b=−(2ER+1),c=−ER.
t=−LRlnx
t=LRln2
t=τln2
t=τln2
where τ=LR.
The correct option is (A) ln2.
Similar Questions
The switch is closed at t=0. Find time after which voltage across capacitor becomes 50 V. (take ln 2 = 0.6)
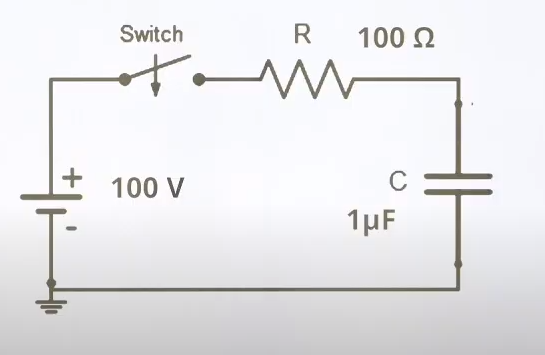 View Solution
View Solution5A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find
Q(c) the rate at which energy is stored in the inductor,View Solution
Knowledge Check
- Question 1 - Select One
If x=12logkb=13logbc=14logcd, then logkd is
A6x3B2x3C12x3D24x3 - Question 2 - Select One
If log 2, log(2n−1) and log(2n+3) are in AP, then n is equal to
A52Blog25Clog35D32 - Question 3 - Select One
The graph between log t1/2 and log a at a given temperature is
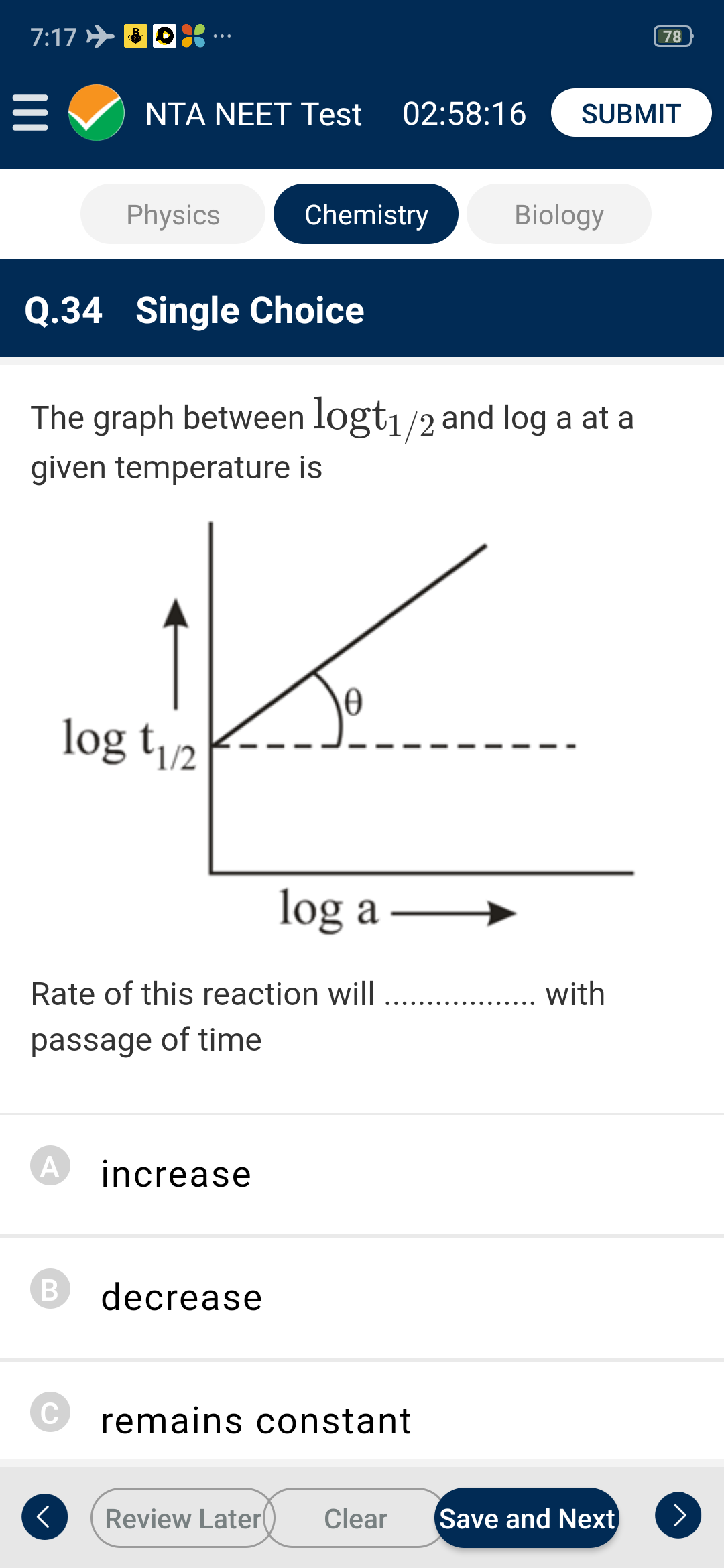
Rate of this reaction will …….with passage of timeAincreaseBdecreaseCremains constantDfirst increase then decrease
Consider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?View Solution2log x-log(x+1)-log(x-1) is equals to
View SolutionIn the circuit diagram shown in the figure the switches S1 and S2 are closed at time t=0.After time t=(0.1)ln2sec, switch S2 is opened.The current in the circuit at time t=0.2n2sec is equal to x32amp.Find out value of x.
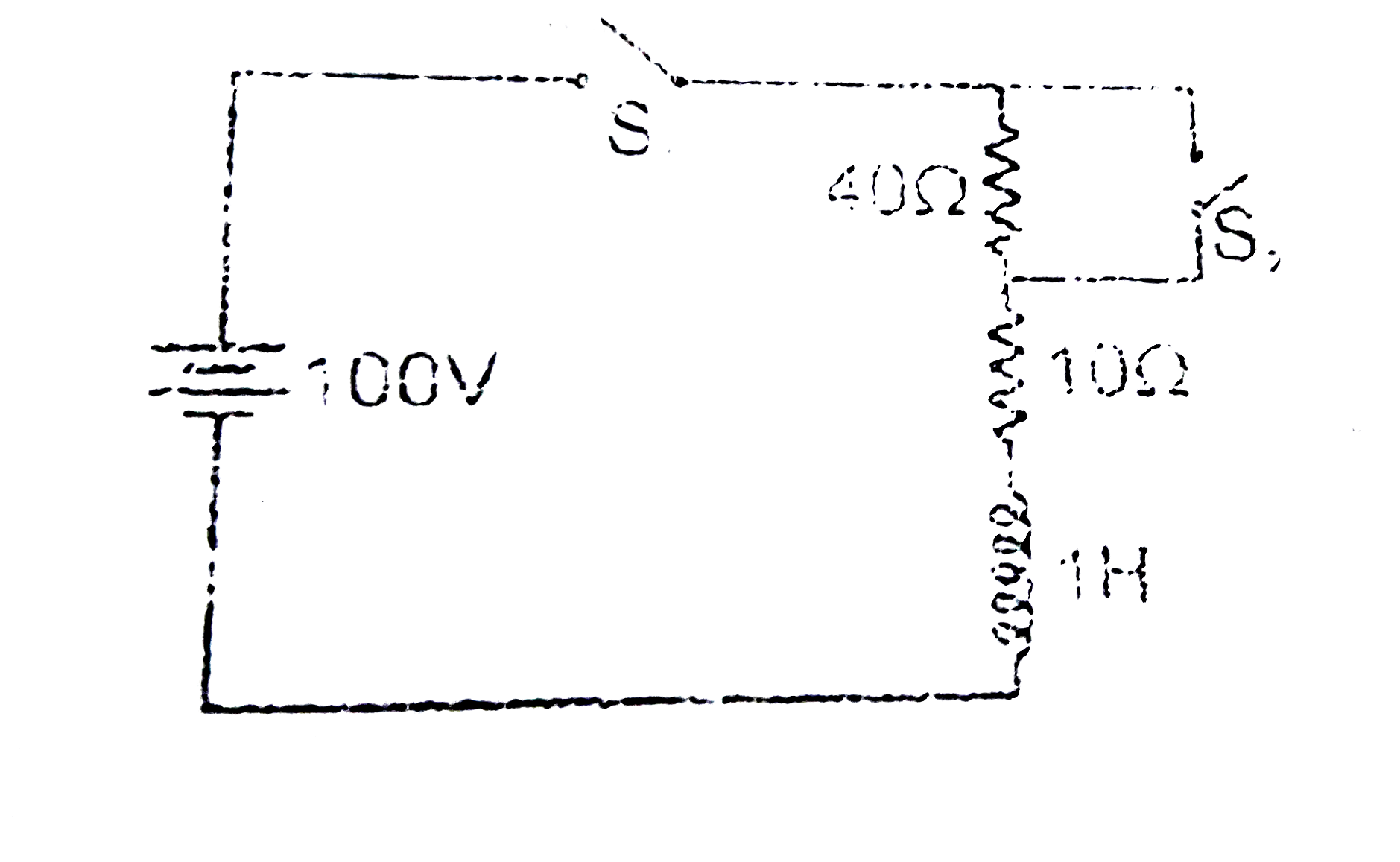 View Solution
View SolutionA graph between log t1/2 and log a (abscissa), a being the initial concentration of A in the reaction A → product, is depicted in the figure. The rate law is
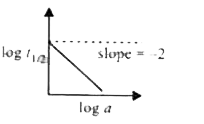 View Solution
View SolutionIf log(a+b2)=12(loga+logb), then a is equal to
View Solution

