An equi-convex glass lens with radius of each face as R is placed in air (.aug=3/2). "If there is water in the object space and air in the image space and given" .auw=4/3, the focal length of the lens is
4 R
2 R
3R2
R
The correct Answer is:C

μ1=43,μ2=32,μ3=1,R1=R,R2=−R
μ3f=μ2−μ1R1+μ3−μ2R2
1f=32−43R+1−32−R=16R+12R=1+36R
f=3R2
Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES67videos
REFLECTION OF LIGHT
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
Similar Questions
Draw ray diagram showing the image formation by a convex lens when an object is placed at twice the focal length of the lens.
View SolutionA convex lens made of a glass of refractive index 3/2 has a focal length 'f' in air. If it is immersed into water of refractive index 4/3, then with calculation, predict the new focal length of the lens inside water.
View Solution
Knowledge Check
- Question 1 - Select One
There is an equiconcave glass lens with radius of each face as R and .aμg=3/2 and .aμW=4/3 . If there is water in object space and air in image space, then the focal length is
A2 RBRC3R/2DR2 - Question 2 - Select One
In the above question if there is air in the object space and water in the image space, then the focal length is
A4 RB2 RC3R2DR - Question 3 - Select One
A fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
A4B6C7.5D9
Draw ray diagrams showing the image formation by a concave lens when an object is placed
(a) between focus and twice the focal length of the lens
(b) beyond twice the focal length of the lensView SolutionAn object is placed at a distance of f2 from a convex lens of focal length f. The image will be
View SolutionA thin equi-convex lens having radius of curvature 10 cm is placed as shown in figure. Calculate focal length of the lens, if parallel rays are incident as shown.
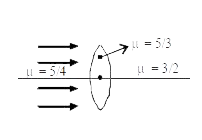 View Solution
View SolutionAn object is placed in front of a thin convex lens of focal length 30cmand a plane mirror is placed15cmbehind the lens.If the final image of the object coincides with the object the distance of the object from the lens is
View SolutionA convex lens forms a virtual image when an object is placed at a distance of 18cm from it. The focal length must be
View Solution

