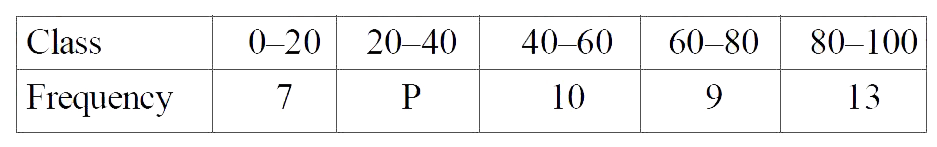If the mean of the following distribution is 6, find the value of p
To find the value of p given that the mean of the distribution is 6, we will follow these steps:
Step 1: Understand the Mean Formula
The mean (¯x) of a frequency distribution is calculated using the formula:
¯x=Σ(xifi)Σfi
where xi is the value of the variable, fi is the frequency, and Σ denotes the summation.
Step 2: Calculate the Total Frequency (Σfi)
We need to find the total frequency by summing all the frequencies provided. Let's assume the frequencies are given as follows:
- Frequency 1: 3
- Frequency 2: 2
- Frequency 3: 3
- Frequency 4: 1
- Frequency 5: 2
Calculating:
Σfi=3+2+3+1+2=11
Step 3: Calculate Σ(xifi)
Next, we calculate Σ(xifi) which is the sum of the product of each value and its corresponding frequency. Assuming the values are:
- x1=2, f1=3 → 2×3=6
- x2=4, f2=2 → 4×2=8
- x3=6, f3=3 → 6×3=18
- x4=10, f4=1 → 10×1=10
- x5=p+5, f5=2 → (p+5)×2=2p+10
Adding these products together:
Σ(xifi)=6+8+18+10+(2p+10)=52+2p
Step 4: Set Up the Equation for the Mean
We know the mean is given as 6. Therefore, we can set up the equation:
6=52+2p11
Step 5: Solve for p
To eliminate the fraction, multiply both sides by 11:
6×11=52+2p
66=52+2p
Now, isolate 2p:
2p=66−52
2p=14
Now, divide by 2:
p=7
Final Answer
The value of p is 7.
---
The mean (¯x) of a frequency distribution is calculated using the formula:
¯x=Σ(xifi)Σfi
where xi is the value of the variable, fi is the frequency, and Σ denotes the summation.
We need to find the total frequency by summing all the frequencies provided. Let's assume the frequencies are given as follows:
- Frequency 1: 3
- Frequency 2: 2
- Frequency 3: 3
- Frequency 4: 1
- Frequency 5: 2
Σfi=3+2+3+1+2=11
Next, we calculate Σ(xifi) which is the sum of the product of each value and its corresponding frequency. Assuming the values are:
- x1=2, f1=3 → 2×3=6
- x2=4, f2=2 → 4×2=8
- x3=6, f3=3 → 6×3=18
- x4=10, f4=1 → 10×1=10
- x5=p+5, f5=2 → (p+5)×2=2p+10
Σ(xifi)=6+8+18+10+(2p+10)=52+2p
We know the mean is given as 6. Therefore, we can set up the equation:
6=52+2p11
To eliminate the fraction, multiply both sides by 11:
6×11=52+2p
66=52+2p
2p=66−52
2p=14
p=7
The value of p is 7.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the mean of the following distribution is 6, then find the value of a.
 A6B7C4D3
A6B7C4D3
If the mean of the following distribution is 6, find the value of 2 4 6 10 3 2 3 1 2
View SolutionIf the mean of the following distribution is 54, find the value of p: Class: 0-20 20-40 40-60 60-80 80-100 Frequency: 7 p 10 9 13
View SolutionFind the mean of the following distribution
View SolutionFind the mean of the following distribution

View SolutionIf the mean of the following distributions 54, find the value of p: Class: 0-20 20-40 40-60 60-80 80-100 Frequency: 7 p 10 9 13
View SolutionFind the mean of the following distribution :

View SolutionFind the mean of the following distribution:
View Solution