A solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

ρ−ρ2ρ1−ρ2
ρ1ρ1−ρ2
ρ1−ρρ1−ρ2
ρ1−ρ2ρ2
The correct Answer is:C
Step by step video, text & image solution for A solid uniform ball having volume V and density rho floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are rho_(1) and rho_(2) respectively, such that rho_(1) lt rho lt rho_(2). What fractio9n of the volume of the ball will be in the lower liquid. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)
24 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A block of material has a density ρ1 and floats three-fourth submerged in a liquid of unknown density. Show tht the density ρ2 of the unknown liquid is given by ρ2=43ρ1.
View SolutionTwo disc has same mass rotates about the same axis with their densities ρ1 and ρ2 respectively such that (ρ1>ρ2), then the relation between I1 and I2 will be
View Solution
Knowledge Check
A solid uniform ball having volume V and density ρ floats at the interface of two unmixable liquids as shown in the figure. The densities of the upper and the lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2 . What fraction of the volume of the ball will be in the lower liquid ?
 Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is
 Aρ2ρ1Bρ2−ρρ2−ρ1Cρ−ρ1ρ2−ρ1Dρ1ρ2
Aρ2ρ1Bρ2−ρρ2−ρ1Cρ−ρ1ρ2−ρ1Dρ1ρ2A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
A(rho-rho_(1))/(rho_(2)-rho)Bρ2−ρρ−ρ1C(rho+rho_(1))/(rho+rho_(2))D(rho+rho_(2))/(rho+rho_(1))
Three liquids of equal masses are taken in three identical cubical vessels A, B and C. Their densities are ρA,ρB and ρC respectively but ρA<ρB<ρC. The force exerted by the liquid on the base of the cubical vessel is
View SolutionThree different liquids are filled in a U-tube as shown in figure. Their densities are ρ1,ρ2 and ρ3 respectively. From the figure we may conclude that
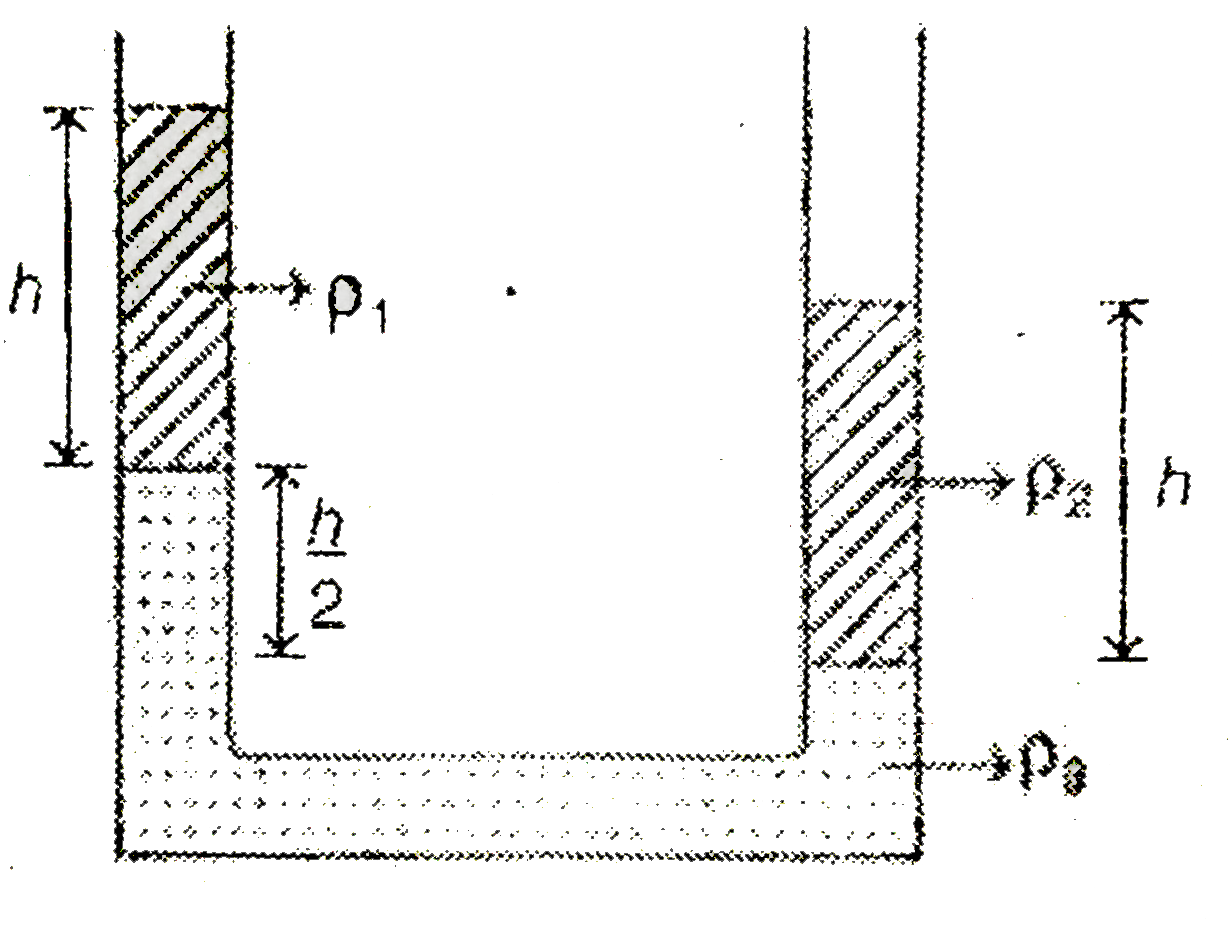
View Solution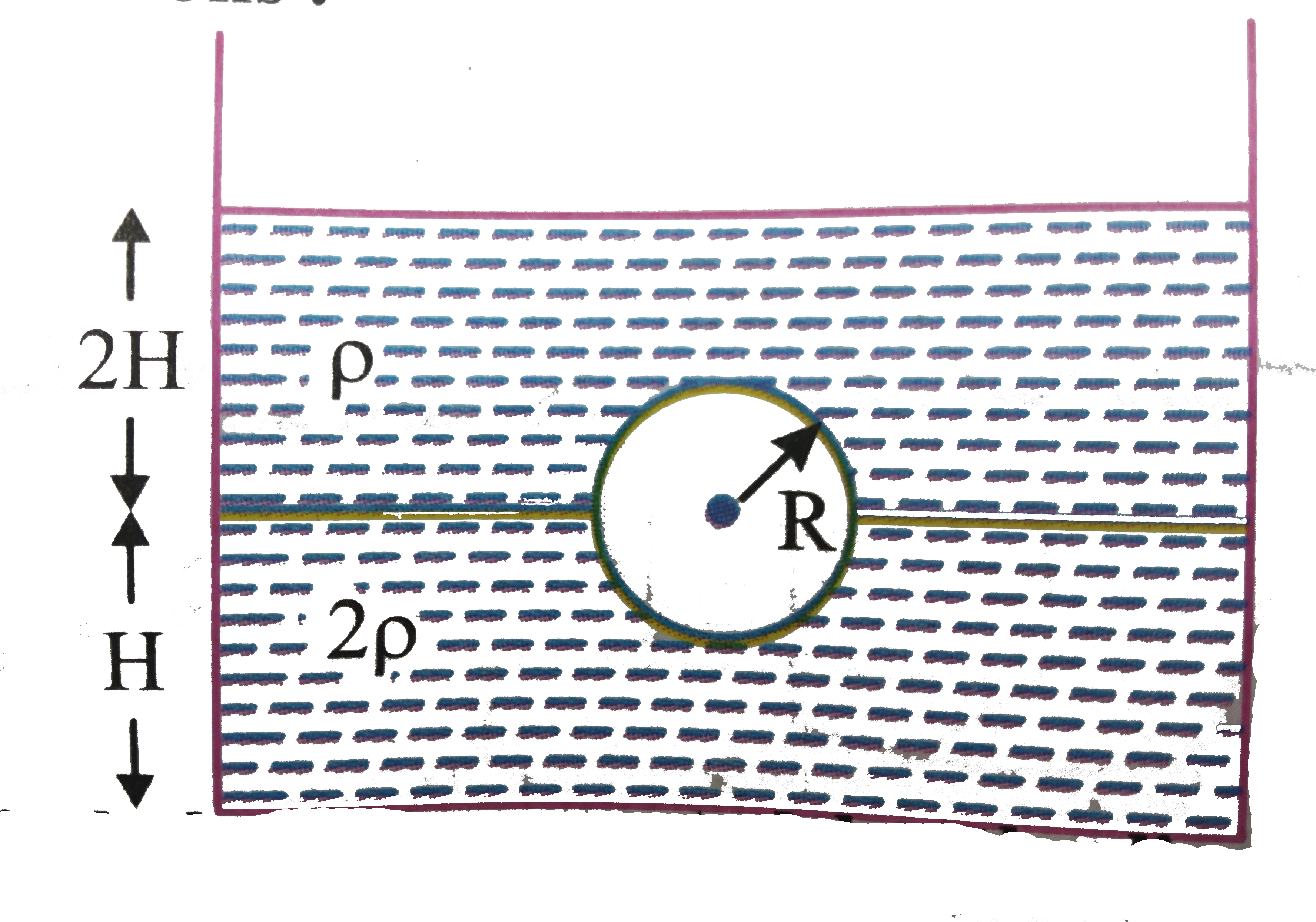
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
If a hole is drilled at the bottom of the vessel then volume of the ball immersed inliquid with density ρ will
View SolutionIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
View SolutionTwo circular discs A and B have equal masses and uniform thickness but have densities ρ1 and ρ2 such that ρ1>ρ2 . Their moments of inertia is
View Solution
