_E01_226_Q01.png)
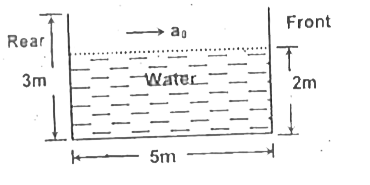
An open retangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side.
(i). Determine the maximum acceleration that can be given without spilling the water.
(ii). Calculate the percentage of water split over if this acceleration of increased by 20%
(iii). If initially the tank is closed at the top and its accelerated horizontally by 9m/s2 find the gauge pressure at the bottom of the front and rear walls of the tank.
The correct Answer is:(i). 4m/s2
(ii). 10%
(iii). 0,45KPa
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 A (Previous year Questions)
29 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)
13 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Viscosity)
3 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
An open rectangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side .
(a) Determine the maximum acceleration that can be given without spilling the water .
View SolutionAn open rectangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side .
(a) Determine the maximum acceleration that can be given without spilling the water .
(b)Calculate the percentage of water spill over , if this acceleration is increased by 20 %

View Solution
Knowledge Check
A closed rectangular tank is completely filled with water and is accelerated horizontally with an acceleration towards the righ. Pressure is i. maximum and ii. minimum at
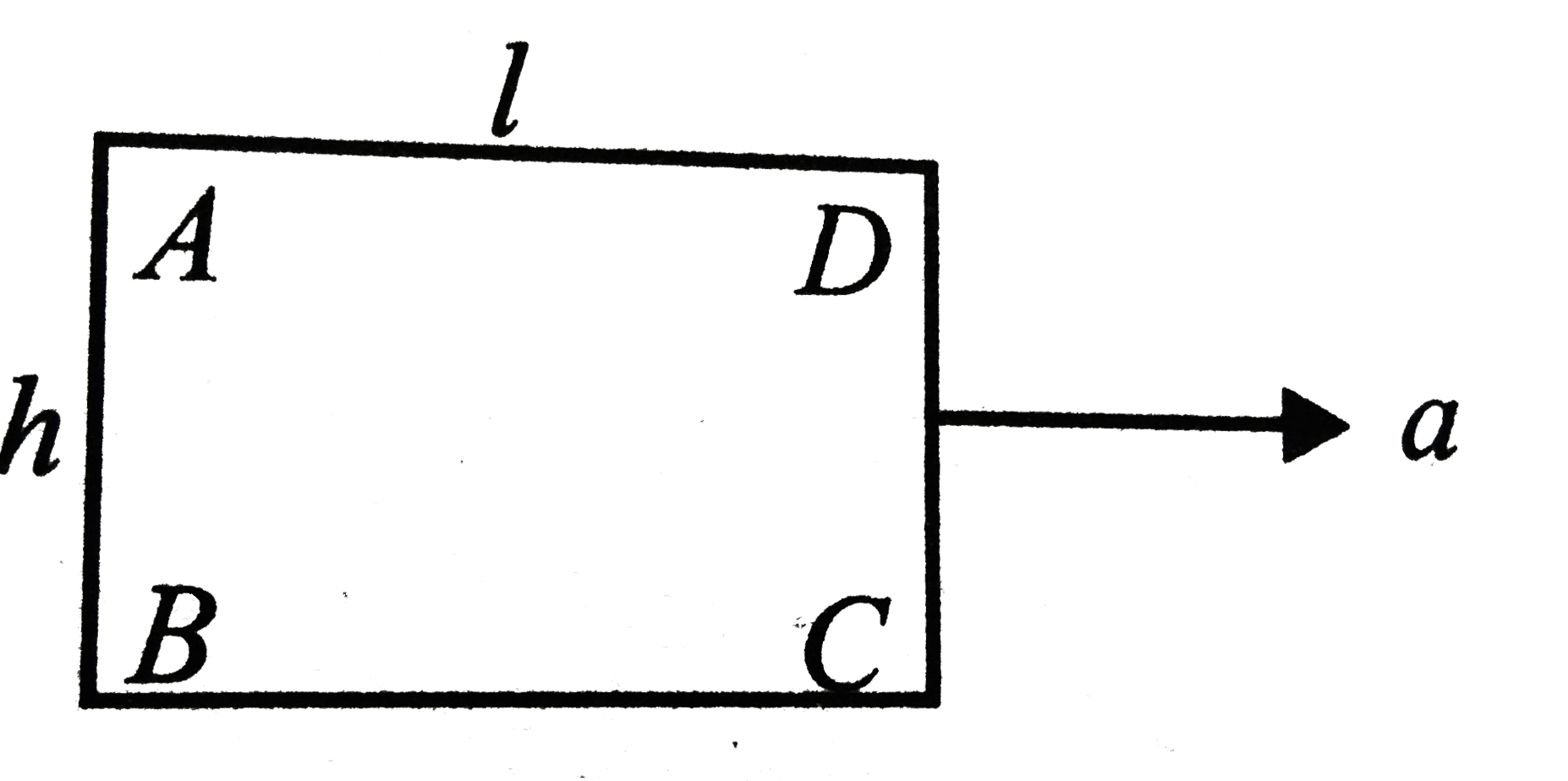 Ai. B ii DBi C ii DCi B ii CDi B ii A
Ai. B ii DBi C ii DCi B ii CDi B ii A
An open reactangular tank with tank with dimensions 5×4m×3m contains water upto a height of 2m is accelerated horizontally along the longer life.
(a) Determine the maximum acceleration that can be given without spilling the water.
(b) If this acceleration is inscreased by 20%. Calculate the percentage of water spilt over.
(c) If initially,the tank is closed at the top and is accelerated horizontally by 9m/s2,find the gauge pressure at the bottom of the front and rear walls of the tank. (g=10m/s2)

View SolutionAn open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.

View Solution.A rectangular water tank is 5m high, 3m long and 2m wide. How many litres water it can hold
View Solution
The pressure at C is
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionA spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
View Solution
