A uniformly tapering conical wire is mae from a material of young's modulus Y and has a normal unextended length L the radii at the upper and lower ends of this conical wire, have values R and 3R, respectively the upper end of the wire is fixed to a rigid support and a mass M is suspended from its lower end. the equilibrium extended length of this wire would equal to:
L(1+19MgπRM3)
L(1+29MgπYR2)
L(1+23MgπYR2)
L(1+13MgπYR2)
The correct Answer is:D
To solve the problem of finding the equilibrium extended length of a uniformly tapering conical wire, we can follow these steps:
Step 1: Understand the Geometry of the Wire
The wire is conical, with the upper radius R and the lower radius 3R. The unextended length of the wire is L.
Step 2: Determine the Radius as a Function of Length
Since the wire tapers, we need to express the radius r at a distance x from the upper end. The relationship can be derived from similar triangles.
Using the geometry:
3R−rL=3R−RL=2RL
From this, we can express r:
r=3R−2RLx
Step 3: Calculate the Extension of a Small Element
Consider a small element of length dx at a distance x from the upper end. The force acting on this element due to the weight M is mg.
The extension dδl of this small element is given by:
dδl=F⋅dxA⋅Y
Where:
- F=mg
- A=πr2=π(3R−2RLx)2
- Y is the Young's modulus.
Thus, we have:
dδl=mg⋅dxπ(3R−2RLx)2Y
Step 4: Integrate to Find Total Extension
To find the total extension δl, we integrate from x=0 to x=L:
δl=∫L0mg⋅dxπ(3R−2RLx)2Y
Step 5: Solve the Integral
Let u=3R−2RLx, then du=−2RLdx or dx=−L2Rdu. The limits change accordingly:
- When x=0, u=3R
- When x=L, u=R
Now substituting:
δl=∫R3Rmg⋅(−L2R)duπu2Y
This simplifies to:
δl=mgL2πY∫3RRduu2
Calculating the integral:
∫duu2=−1u
Thus:
δl=mgL2πY(−1u)3RR=mgL2πY(−13R+1R)=mgL2πY(23R)
So:
δl=mgL3πYR
Step 6: Find the Total Extended Length
The total extended length L′ is the original length plus the extension:
L′=L+δl=L+mgL3πYR=L(1+mg3πYR)
Final Answer
The equilibrium extended length of the wire is:
L′=L(1+mg3πYR)
The wire is conical, with the upper radius R and the lower radius 3R. The unextended length of the wire is L.
Since the wire tapers, we need to express the radius r at a distance x from the upper end. The relationship can be derived from similar triangles.
3R−rL=3R−RL=2RL
From this, we can express r:
r=3R−2RLx
Consider a small element of length dx at a distance x from the upper end. The force acting on this element due to the weight M is mg.
dδl=F⋅dxA⋅Y
Where:
- F=mg
- A=πr2=π(3R−2RLx)2
- Y is the Young's modulus.
dδl=mg⋅dxπ(3R−2RLx)2Y
To find the total extension δl, we integrate from x=0 to x=L:
δl=∫L0mg⋅dxπ(3R−2RLx)2Y
Let u=3R−2RLx, then du=−2RLdx or dx=−L2Rdu. The limits change accordingly:
- When x=0, u=3R
- When x=L, u=R
δl=∫R3Rmg⋅(−L2R)duπu2Y
This simplifies to:
δl=mgL2πY∫3RRduu2
Calculating the integral:
∫duu2=−1u
Thus:
δl=mgL2πY(−1u)3RR=mgL2πY(−13R+1R)=mgL2πY(23R)
So:
δl=mgL3πYR
The total extended length L′ is the original length plus the extension:
L′=L+δl=L+mgL3πYR=L(1+mg3πYR)
The equilibrium extended length of the wire is:
L′=L(1+mg3πYR)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)13videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Multiple correct answers)2videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 B (Bran storming Subjective Exercise)15videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View Solution
Knowledge Check
- Question 1 - Select One or More
A metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
AThe loss in gravitational potential energy of mass M is Mgl.BThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is loss of mechanical energy of system is 12Mgl - Question 2 - Select One or More
A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
ALoss in gravitational potential energy ofM is MglBThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is 12Mgl - Question 3 - Select One
A wire of natural length l, young's modulus Y and ares of cross-section A is extended by x. Then, the energy stored in the wire is given by
A12YAlx2B13YAlx2C12YlAx2D12YAl2x2
The mass and length of a wire are M and L respectively. The density of the material of the wire is d. On applying the force F on the wire, the increase in length is l, then the Young's modulus of the material of the wire will be
View SolutionIn an experiment to determine the Young's modulus of the material of a wire, the length of the wire and the suspended mass are doubled. Then the Young's modulus of the wire
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionA wire of length L and density ρ and Young's modulus Y is hanging from a support. Find the elongation in the length of wire at which wire will break:
View SolutionTwo wires of the same material (Young's modulus=Y) and same length L but radii R and 2R respectively are joined end to end and a weight w is suspended from the combination as shown in the figure. The elastic potential energy in the system is
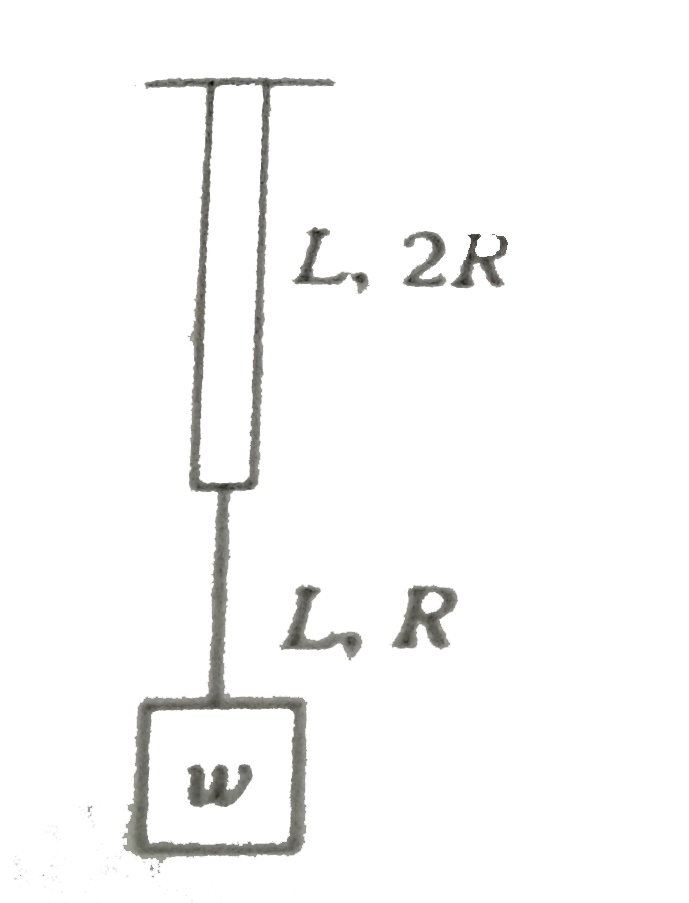 View Solution
View Solution

