Thin films, including soap bubbles and oil slicks, show patterns of al

Consider interference between two sources of intensity I and 4I. Find out resultant intensity where phase difference is (i). $π / 4$
(ii). $π$
(iii). $4 π$

View Solution

Two identical monochromaticlight sources A & B intensity $10^{- 15} W / m^{2}$ produce wavelength of light $4000 \sqrt{3} Å$ A glass of thickness 3mm is placed in the path of the ray as shown in figure the glass has a varible refractive index $n = 1 + \sqrt{x}$ where x (in mm) is distance of plate from left to right calculate total intensity at focal points F of the lens.
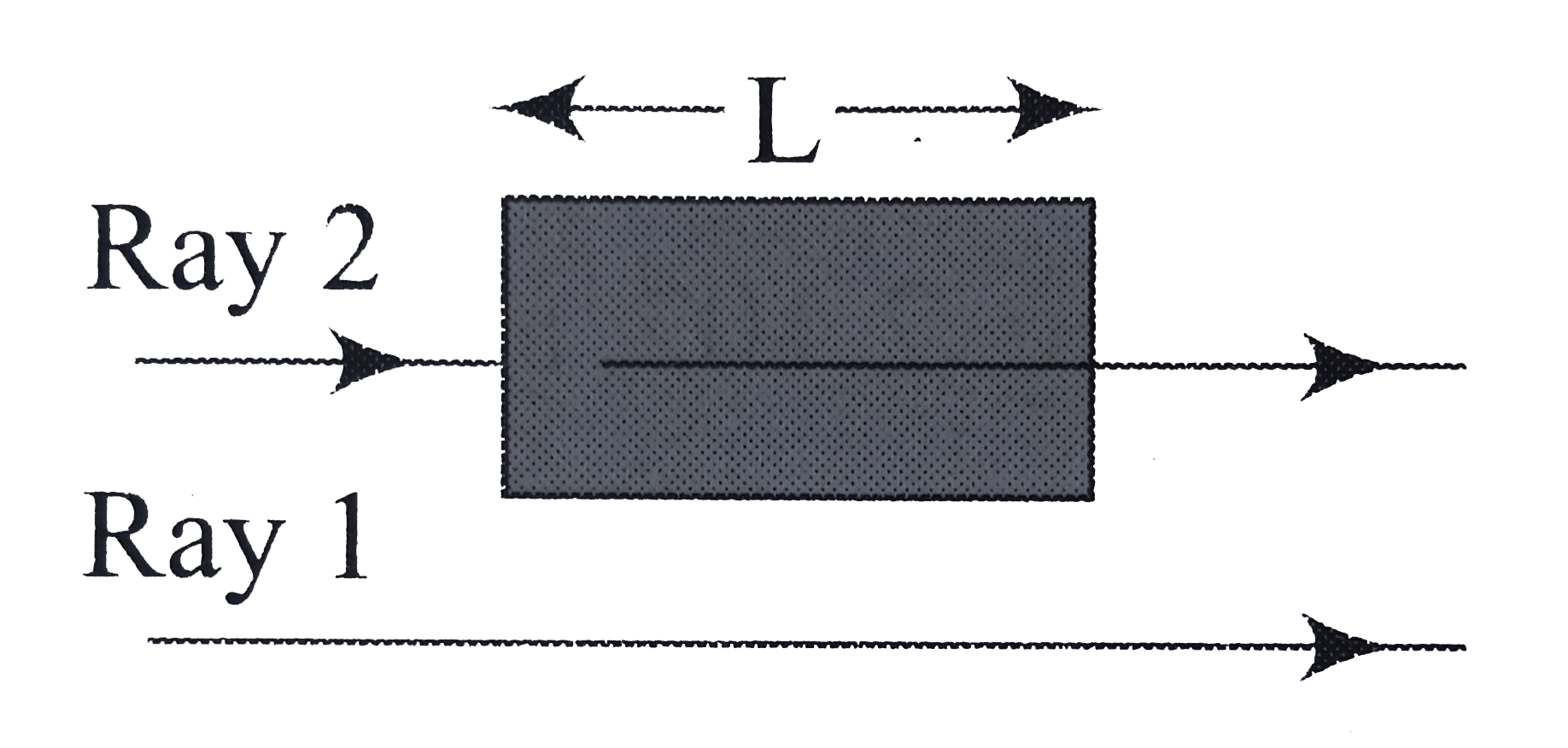
ocr_image

View Solution

As shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is $N_{2}$ for Ray 2 and $N_{1}$ for Ray 1. In the following table, values of $N_{1}$ and $N_{2}$ are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
$N_{1}$ 2.75 1.80 3.00 3.25
$N_{2}$ 2.75 2.80 3.25 4.00
ocr_image

View Solution

Match List I with List II and select the correct answer using the codes given below the lists :
ocr_image

View Solution

Thin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength $(180^{\circ})$ , the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray $R_{a}$ and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray $R_{c}$ .
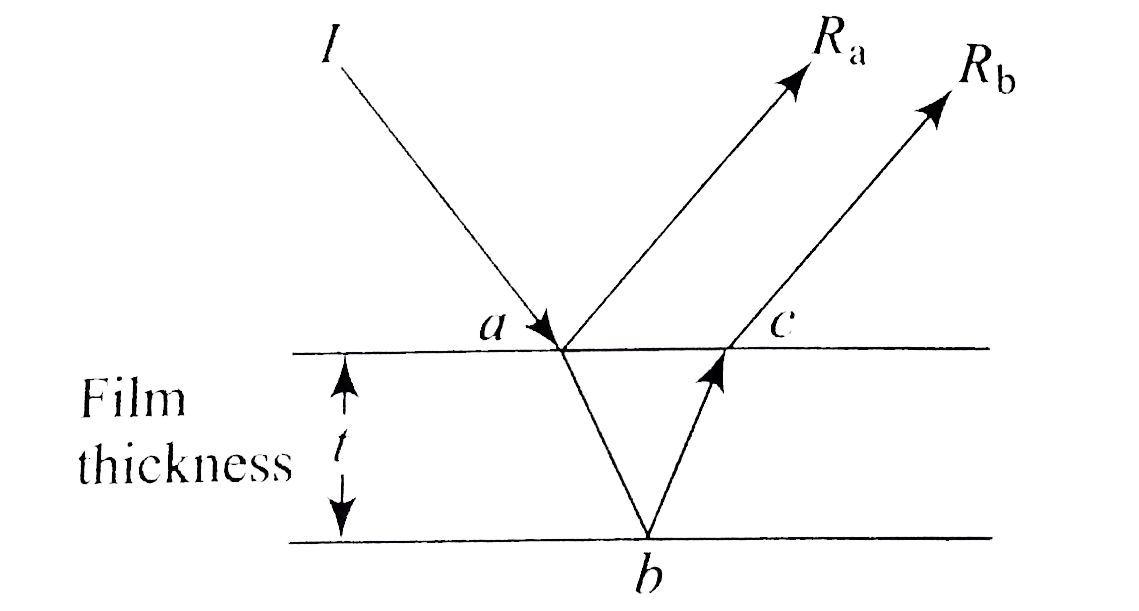
ocr_image
$R_{a}$ and $R_{c}$ are parallel. However, $R_{c}$ has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If $R_{a}$ and $R_{c}$ are in phase, they will undergo constructive interference and the region ac will be bright. If $R_{a}$ and $R_{c}$ are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if $n_{1} > n_{2}$ , the reflected wave will change phase. If $n_{1} < n_{2}$ , the reflected wave will not undergo a phase change.
For reference, $n_{a i r} = 1.00$ .
ocr_image
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when $2 t = m λ / n, m = 0, 1, 2, 3$ ,...
Destrcutive interference occurs when $2 t = (m + \frac{1}{2}) \frac{λ}{n}$ ,
$m = 0, 1, 2, 3$ ,...
If the waves are $180^{\circ}$ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
$2 t = (m + \frac{1}{2}) \frac{λ}{n}, m = 0, 1, 2, 3$ ,...
Destructive interference occurs when
$2 t = \frac{m λ}{n}, m = 0, 1, 2, 3$ ,...
72. A film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?

View Solution

Thin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength $(180^{\circ})$ , the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray $R_{a}$ and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray $R_{c}$ .
ocr_image
$R_{a}$ and $R_{c}$ are parallel. However, $R_{c}$ has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If $R_{a}$ and $R_{c}$ are in phase, they will undergo constructive interference and the region ac will be bright. If $R_{a}$ and $R_{c}$ are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if $n_{1} > n_{2}$ , the reflected wave will change phase. If $n_{1} < n_{2}$ , the reflected wave will not undergo a phase change.
For reference, $n_{a i r} = 1.00$ .
ocr_image
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when $2 t = m λ / n, m = 0, 1, 2, 3$ ,...
Destrcutive interference occurs when $2 t = (m + \frac{1}{2}) \frac{λ}{n}$ ,
$m = 0, 1, 2, 3$ ,...
If the waves are $180^{\circ}$ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
$2 t = (m + \frac{1}{2}) \frac{λ}{n}, m = 0, 1, 2, 3$ ,...
Destructive interference occurs when
$2 t = \frac{m λ}{n}, m = 0, 1, 2, 3$ ,...
A thin film with index of refraction 1.33 coats a glass lens with index of refraction 1.50. Which of the following choices is the smallest film thickness that will not reflect light with wavelength 640 nm?

View Solution

Thin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength $(180^{\circ})$ , the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray $R_{a}$ and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray $R_{c}$ .
ocr_image
$R_{a}$ and $R_{c}$ are parallel. However, $R_{c}$ has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If $R_{a}$ and $R_{c}$ are in phase, they will undergo constructive interference and the region ac will be bright. If $R_{a}$ and $R_{c}$ are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if $n_{1} > n_{2}$ , the reflected wave will change phase. If $n_{1} < n_{2}$ , the reflected wave will not undergo a phase change.
For reference, $n_{a i r} = 1.00$ .
ocr_image
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when $2 t = m λ / n, m = 0, 1, 2, 3$ ,...
Destrcutive interference occurs when $2 t = (m + \frac{1}{2}) \frac{λ}{n}$ ,
$m = 0, 1, 2, 3$ ,...
If the waves are $180^{\circ}$ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
$2 t = (m + \frac{1}{2}) \frac{λ}{n}, m = 0, 1, 2, 3$ ,...
Destructive interference occurs when
$2 t = \frac{m λ}{n}, m = 0, 1, 2, 3$ ,...
A soap film of thickness t is surrounded by air and is illuminated at near normal incidence by noonochromatic light wavelength $λ$ in the film. With respect to the wavelength of the monochromatic ligth in the film, what film thickness will produce maximum consturctive interference

View Solution

Two identical sinusoidal waves, moving in same direction along a stretched string, interfere, with each other. The amplitude of each wave is 10.0mm, and the phase difference between them is 80^(@) . What is the amplitude of the resultant wave and the nature of interference ?

View Solution

Thin films, including soap bubbles and oil slicks, show patterns of alternating dark and bright regions resulting from interference among the reflected light waves. If two waves are in phase their crest and troughs will coincide. The interference will be constructive and the aplitude of the resultant wave will be greater than the amplitude of either constituent wave. if the two waves are out of phase, the crests of one wave will coincide with the troughs of the other wave. The interference will be destructive and the amplitude of the resultant wave will be less than that of either constituent wave. at the interface between two transparent media some light is reflected and some light is refracted. * When incident light, reaches the surface at point a, some of the light is reflected as ray R_(a) and and some is refracted following the path ab to the back of the film. *At point b some of the light is refracted out of the film and part is reflected back refracted out of the fiml as ray R_(c) . R_(a) and R_(c) are parallel. However, R_(c) has travelled the extra distance within the film of abc. if the angle of incidence is small then abc is approximately twice the film's thickness. if R_(a) and R_(c) are in phase they will undergo constructive interference and the region ac will be bright if R_(a) and R_(c) are out of phase, they will undergo destructive interference. * Refraction at an interface never changes the phase of the wave. * For reflection at the interface between two media 1 and 2, if n_(1)ltn_(2) the reflected wave will change phase by pi . if n_(1)gtn_(2) the reflected wave will not undergo a phase change. for reference n_(air)=1.00 * if the waves are in phase after refection at all interfaces, then the effects of path length in the film are Constructive interference occur when (n= refractive index) 2t=mlamda//n" "m=0,1,2,3... .. Destructive interference occurs when 2t=(m+1//2)lamda//n" "m=0,1,2,3... Q. A 600 nm light is perpendicularly incident on a soap film suspended in air. The film is 1.00 mum thick with n=1.35. Which statement most accurately describes the interference of the light reflected by the two surfaces of the film?

View Solution

यदि सामान आयाम a की दो प्रकाश तरंगो के व्यतिकरण से परिणामी तरंग का आयाम a ही प्राप्त हो तब दोनों तरंगो के मध्य कालान्तर क्या होगा?

View Solution

Two waves of equal amplitude when superposed, give a resultant wave having an amplitude equal to that of either wave. The phase difference between the two waves is

View Solution

If two waves with the amplitude of E_(0) each undergo constructive interference, the amplitude of the resulting wave is

View Solution

What is the phase difference between consecutive crest and through ?

View Solution

Find the amplitude of the resultant wave produced due to interference of two wavesand what will be resultant amplitude when thewaves are. in phase and

View Solution

When a crest of one wave coincides the crest of other wave, the resultant amplitude is maximum at the point, then that point looks:

View Solution

The correct Answer is:B

$t = 350 n m, n = 1.35$
$2 n t - \frac{λ}{2} = \frac{m a λ}{2} (m = 1, 3, 5, . .)$
$t = \frac{(m + 1) \frac{λ}{2}}{2 \times 1.35} = 350 n m$
$λ = \frac{350 \times 2.7 \times 2}{(m + 1)} = \frac{945 \times 2}{m + 1}$
For $m = 1, 3, 5, λ = 945, 473$ …

Topper's Solved these Questions

Similar Questions

ALLEN-WAVE OPTICS-Exercise 3 (Miscellaneous type Questions)

The correct Answer is:B

t=350nm,n=1.35 2nt−λ2=maλ2(m=1,3,5,..) t=(m+1)λ22×1.35=350nm λ=350×2.7×2(m+1)=945×2m+1 For m=1,3,5,λ=945,473 …

Topper's Solved these Questions

Similar Questions

ALLEN-WAVE OPTICS-Exercise 3 (Miscellaneous type Questions)

$t = 350 n m, n = 1.35$
$2 n t - \frac{λ}{2} = \frac{m a λ}{2} (m = 1, 3, 5, . .)$
$t = \frac{(m + 1) \frac{λ}{2}}{2 \times 1.35} = 350 n m$
$λ = \frac{350 \times 2.7 \times 2}{(m + 1)} = \frac{945 \times 2}{m + 1}$
For $m = 1, 3, 5, λ = 945, 473$ …