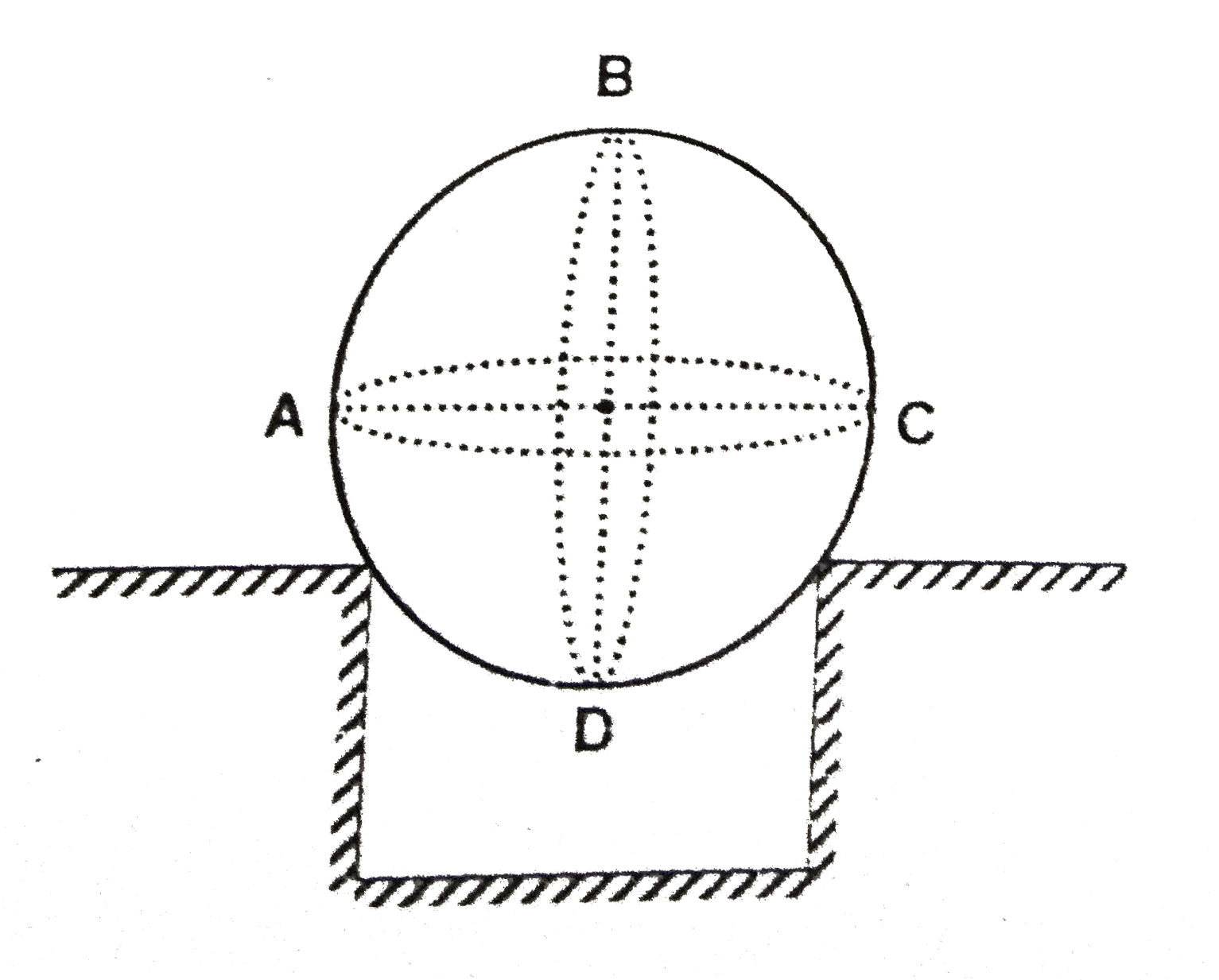
A sphere of mass m and radius r rolls without slipping over a tunnel of width d=8r5 as shown in the figure. (in the figure the sphere rolls perpendicular to the plane of the page) the velocity of centre of mass of sphere is v directed into the plane of the page. the maximum speed of a point on the sphere is
4v3
8v3
6v3
3v2
The correct Answer is:B
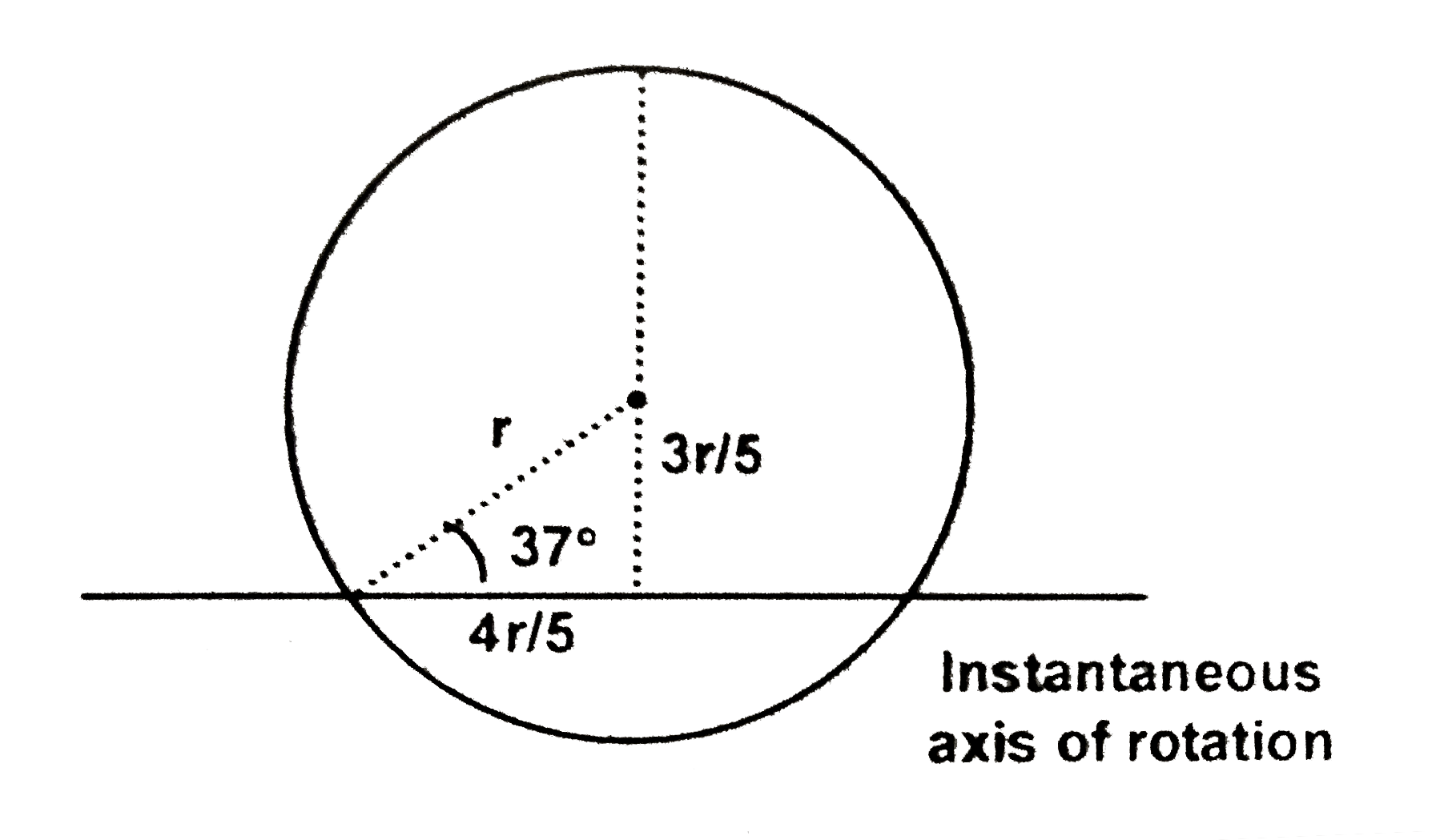
v=ω×3r5⇒ω=5v3r
vB=ω×8r5=5v3r×8r5=8v3
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
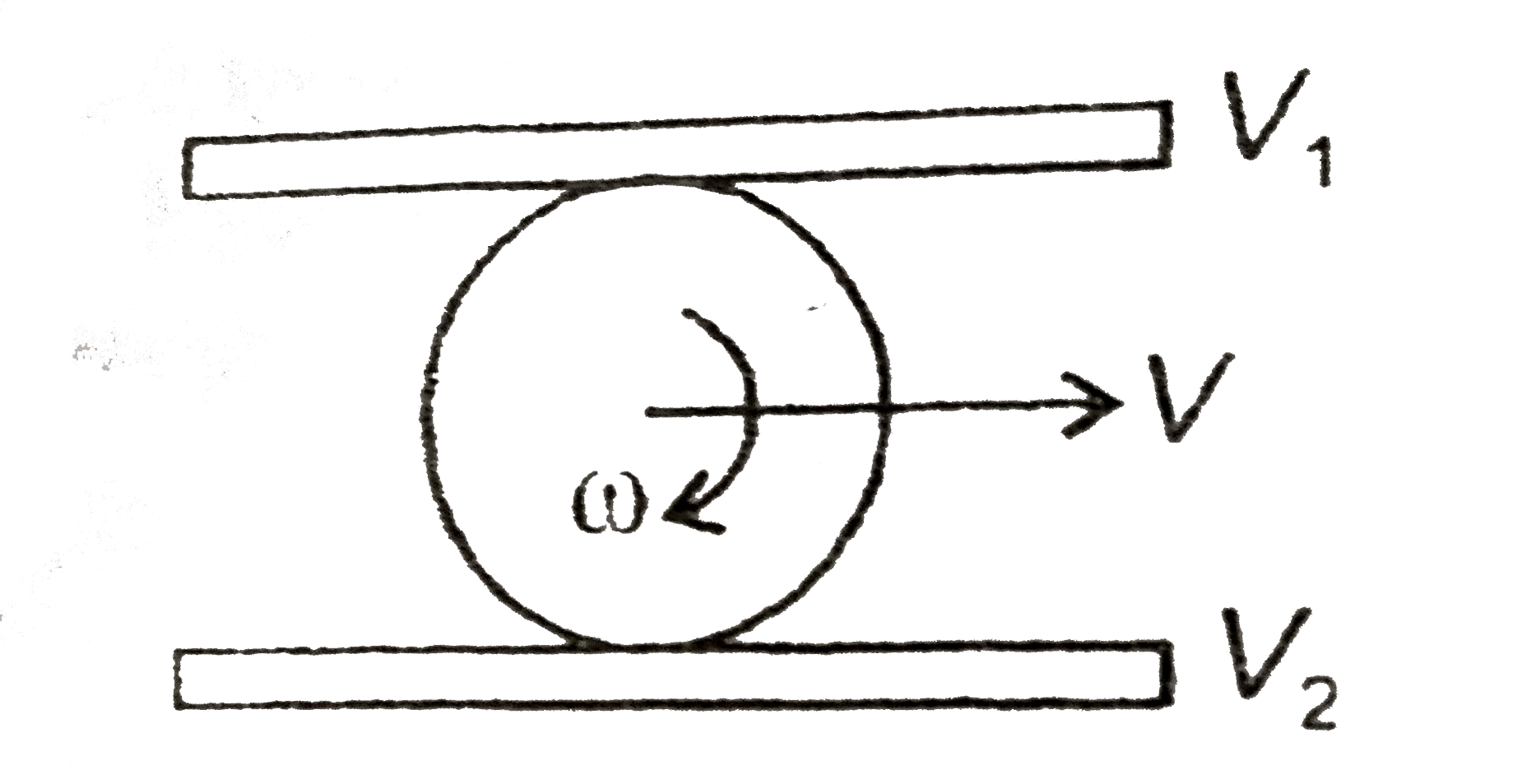
A sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere

View Solution
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.If a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
A140 JB280 JC0.014 JD0.028 JA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
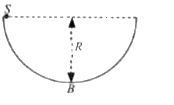 AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2

A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA solid sphere of mass M and radius R, rolling down a smooth inclined plane, without slipping, reaches the bottom with a velocity v. What is the height of the inclined plane in terms of the velocity v ?

View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution
