A particle whose velocity is given as →v=ˆi+6tˆjm/s is moving in x-y plane. At t-0, particle is at origin. Find the radius of curvature of path at point (√23m,23m)
1.5 m
3.0 m
4.5 m
6.0 m
The correct Answer is:C
vx=1⇒x=t and vy=6t⇒y=3t2⇒y=3x2
⇒dydx=6x,d2ydx2=6⇒∣∣∣dydx∣∣∣x=√23=2√2
As we know that
R=[1+(dydx)2]3/2d2ydx2=(1+8)3/26=4.5m
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
If equation of path of moving particle is given by y=2x2 ,radius of curvature of path of particle at origin is
View SolutionA particle starts moving with velocity "vecV=hat i(m/s)", and acceleration "vec a=(hat i+hat j)(m/s^(2))".Find the radius of curvature of the particle at "t=1sec".
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows the graph of velocity versus time for a particle going along x axis. Initially at t = 0, particle is at x = 3m. Find position of particle at t = 2s. (in m)
 A9mB3mC12mD6m
A9mB3mC12mD6m - Question 2 - Select One
A particle moves in plane with acceleration →a=2ˆi+2ˆj. If →v=3ˆi+6ˆj, then final velocity of particle at time t=2s is
A5ˆi+8ˆjB7ˆi+10ˆjC2ˆi+6ˆjD3ˆi+2ˆj
A particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
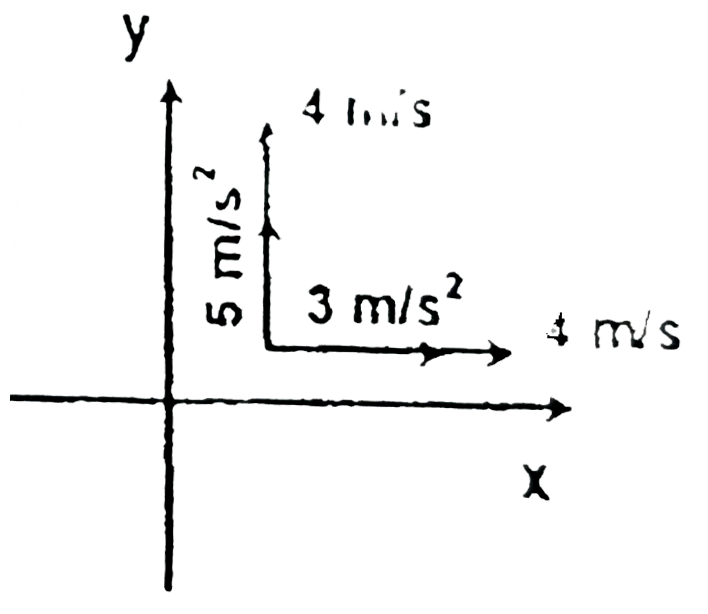 View Solution
View SolutionA particle is given an initial velocity of →u=(3ˆi+4ˆj)m/s. Acceleration of the particle is →a=(3t2+2tˆj)m/s2. Find the velocity of particle at t=2s.
View SolutionThe velocity of an object is given by →v=(6t3ˆi+t2ˆj)m/s) . Find the acceleration at t = 2s.
View SolutionInstantaneous velocity of a particle moving in +x direction is given as v=3x2+2. At t=0, particle starts from origin. Find the average velocity of the particle between the two points p(x=2) and Q(x=4) of its motion path.
View SolutionA particle moves in xy plane with a velocity given by →V=(8t−2)ˆi+2ˆj.. If it passes through the point (14,4) at t=2 sec , then give eqution of the point
View SolutionMotion of Mass Center in Vector Form
A 2.0 kg particle has a velocity of Vecv_1=(2.0hati-3.0hatj)m /s, and a 3.0 kg particle has a velocity vecv_2=(1.0hati+6.0hatj)m/s.
(a) How fast is the center of mass of the particle system moving?
(b) Find velocities of both the particles in centroidal frame.View Solution

