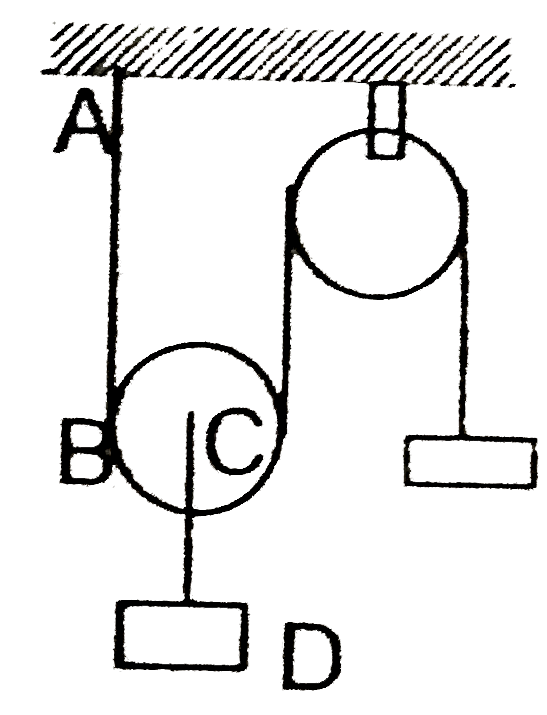
Both the strings shown in figure are mode of same material and have same cross-section. The pulleys are light the wave speed of a transverse wave in the string AB is $v_{1}$ and in CD it is $v_{2}$ . Then $v_{1} / v_{2}$ is

A

1

B

2

C

$\sqrt{2}$

D

$1 / \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$v = \sqrt{\frac{T}{μ}} : V_{A B} = \sqrt{\frac{T}{μ}}, V_{C D} = \sqrt{\frac{2 T}{μ}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747videos
TEST PAPERS
BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20videos
SIMPLE HARMONIC MOTION
BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5videos
WORK, ENERGY AND POWER

Similar Questions

Knowledge Check

Question 1 - Select One
Both the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string $A B$ is $v_{1}$ and in $C D$ it is $v_{2}$ , the $v_{1} / v_{2}$ is

A $1$
B $2$
C $\sqrt{2}$
D $\frac{1}{\sqrt{2}}$
Question 2 - Select One
Both strings shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is $v_{1} and \in C D i t i s v_{2}$ . Then $\frac{v_{1}}{v_{2}}$ is

A1
B2
C $\sqrt{2}$
D $\frac{1}{\sqrt{2}}$
Question 3 - Select One
both the strings , shown in figure are made of same material and have same cross - section. The pulleys are light the wave speed pf a travsverse wave in the string AB is $v_{1}$ and in CD is $v_{2}$ . The ratio $v_{1} / v_{2}$ is

A1
B2
C $\sqrt{2}$
D $1 \sqrt{2}$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile