A uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
3g/2L,3g/2
3g/2L,g
g/2L,g/2
6g/L,6g
The correct Answer is:A
The figure shown the rod at an angle θ to the vertical. If we take torques about the pivot we need not be concerned with the force due to the pivot. The torque due to the weight is 1/2mgLsinθ, so the second law for the rotational motion is.
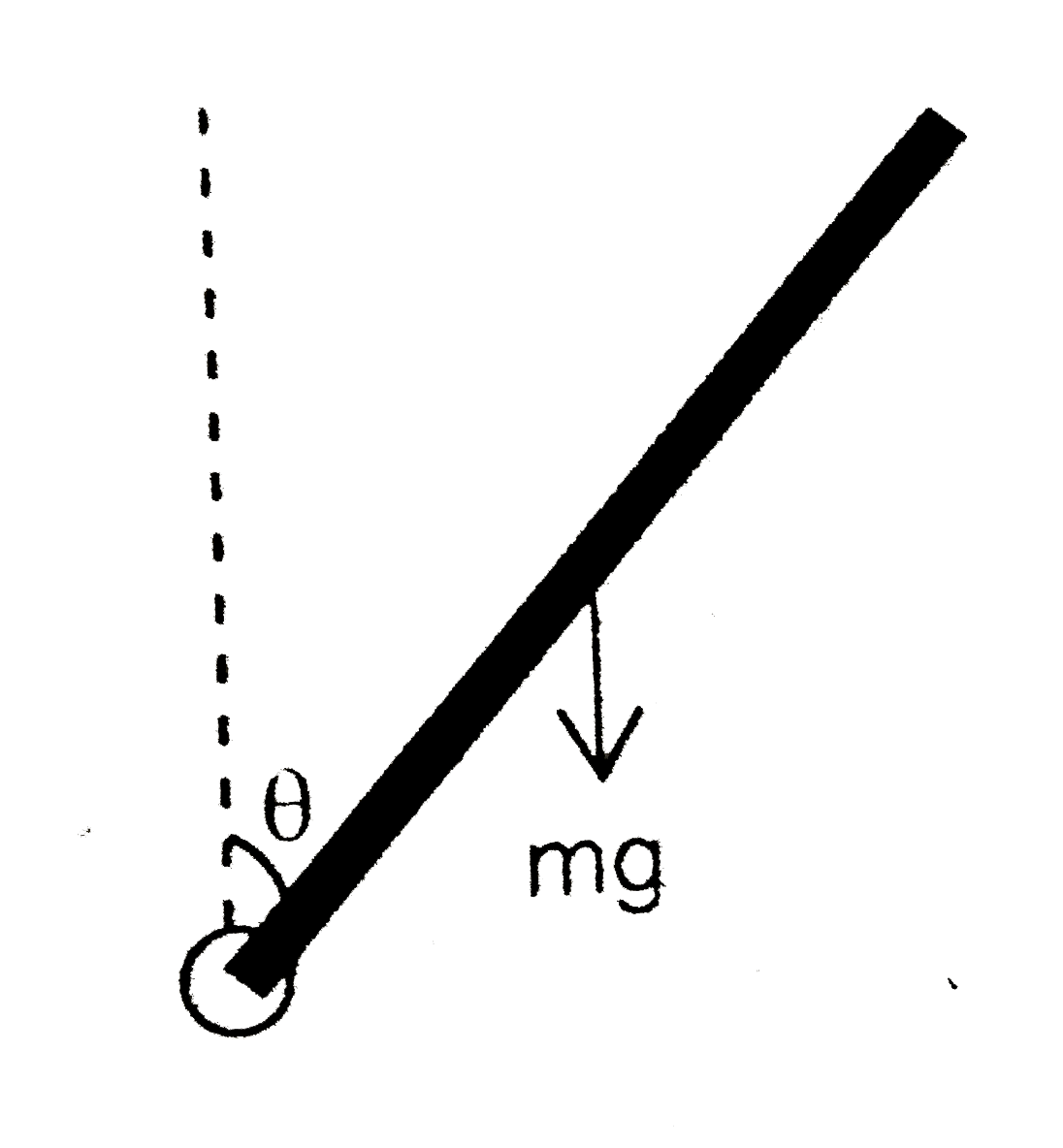
mgL2sinθ=ML23α
Thus α=3gsinθ2L
When the rod is horizontal θ=π/2 and α=3g/2L
Tangential linear acceleration of the free end is at=αL=3g2
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
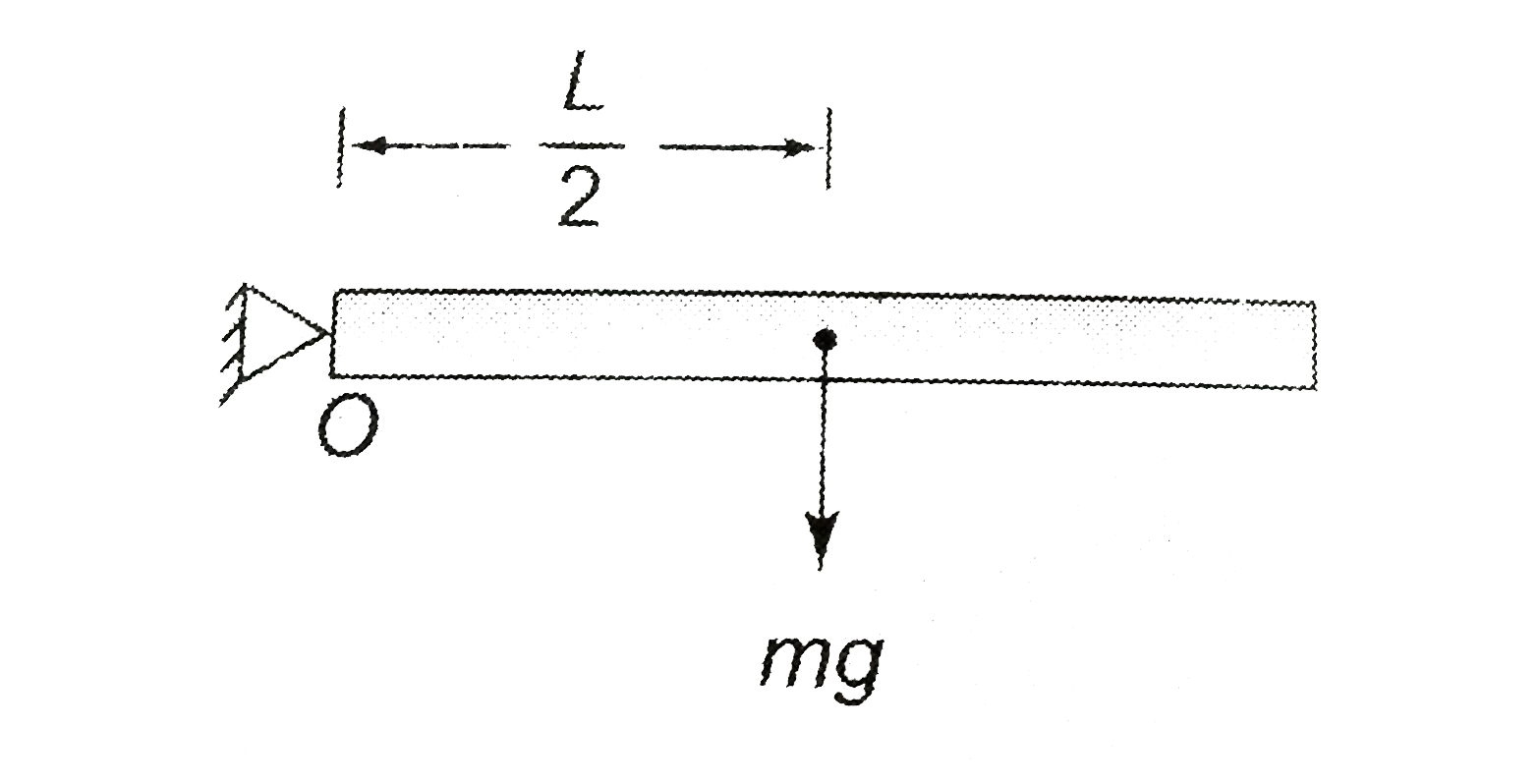
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View Solution
Knowledge Check
A uniform rod of mas m and length l is made to stand at an angle of 60∘ with the vertical. What is the potential energy of the rod in this position?
AmglBmgl2Cmgl3Dmgl4A rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gLA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 A2√5g7lB2√6g7lC√3g7lD2√gl
A2√5g7lB2√6g7lC√3g7lD2√gl
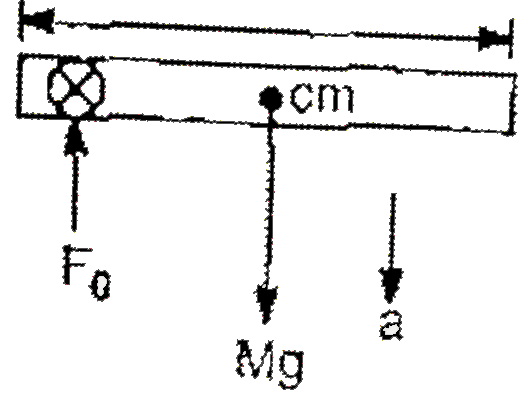
A uniform slender rod of length L and mass M is pivoted at one end. It is held horizontal and releasaed. Assume the pivot is frictionless. Find .
(a) the angular acceleration of the rod immediately after it is released, and
(b) the force F0 exerted on the rod by the pivot immediately after release.
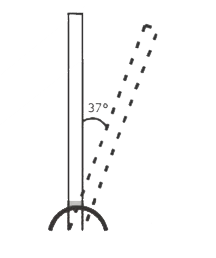
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
View Solution