If a stone is relased from a balloon moving upwards with certain velocity v0 at certain height above earth's surface then velocity time curve of stone's motion can be best represented by : (g = constant)
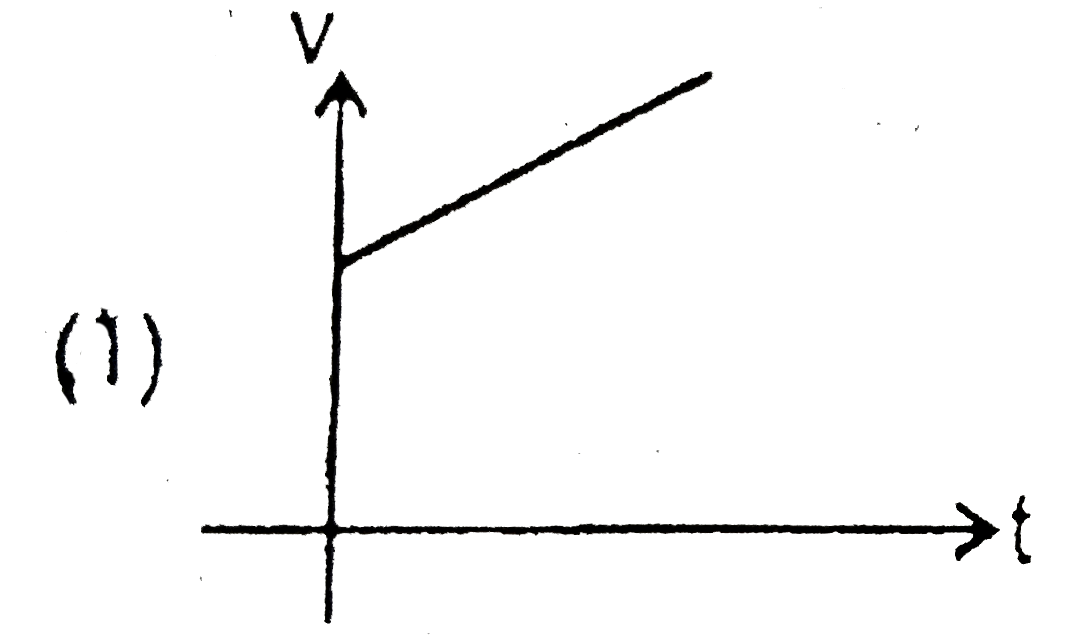
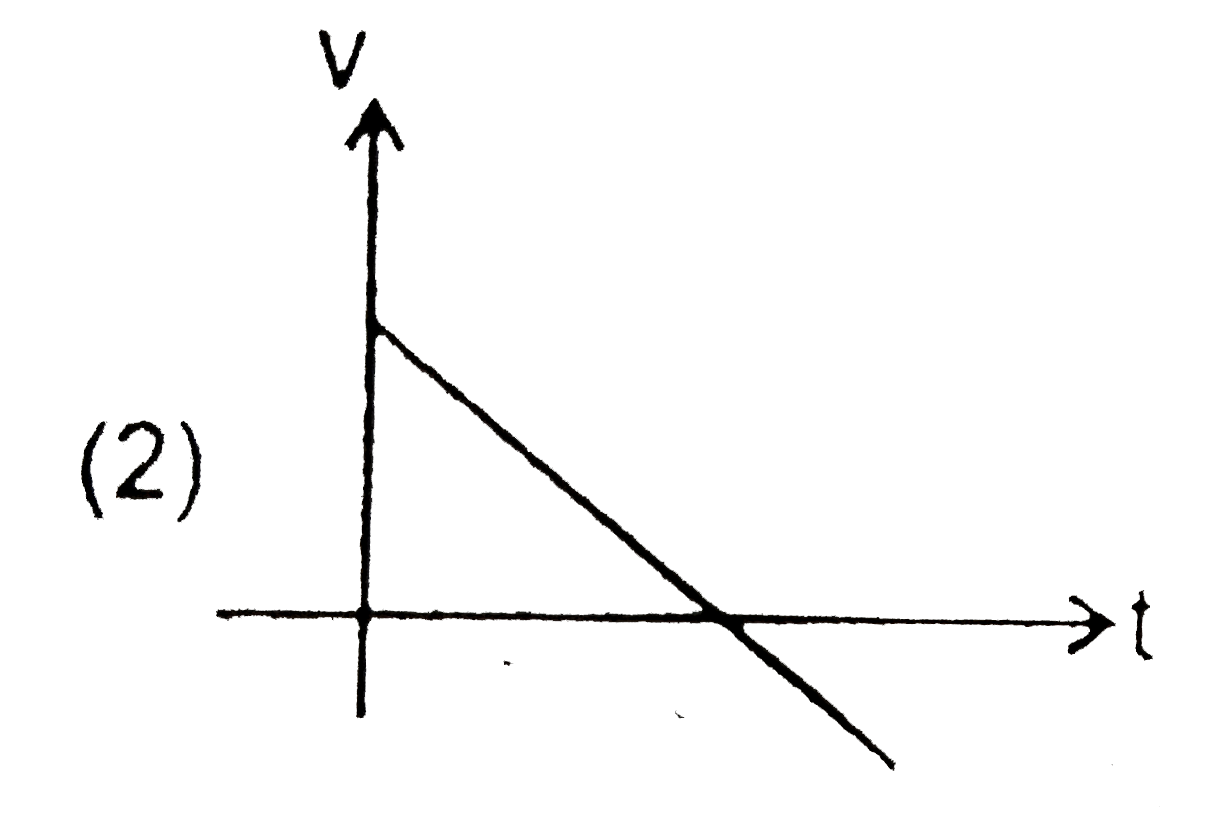
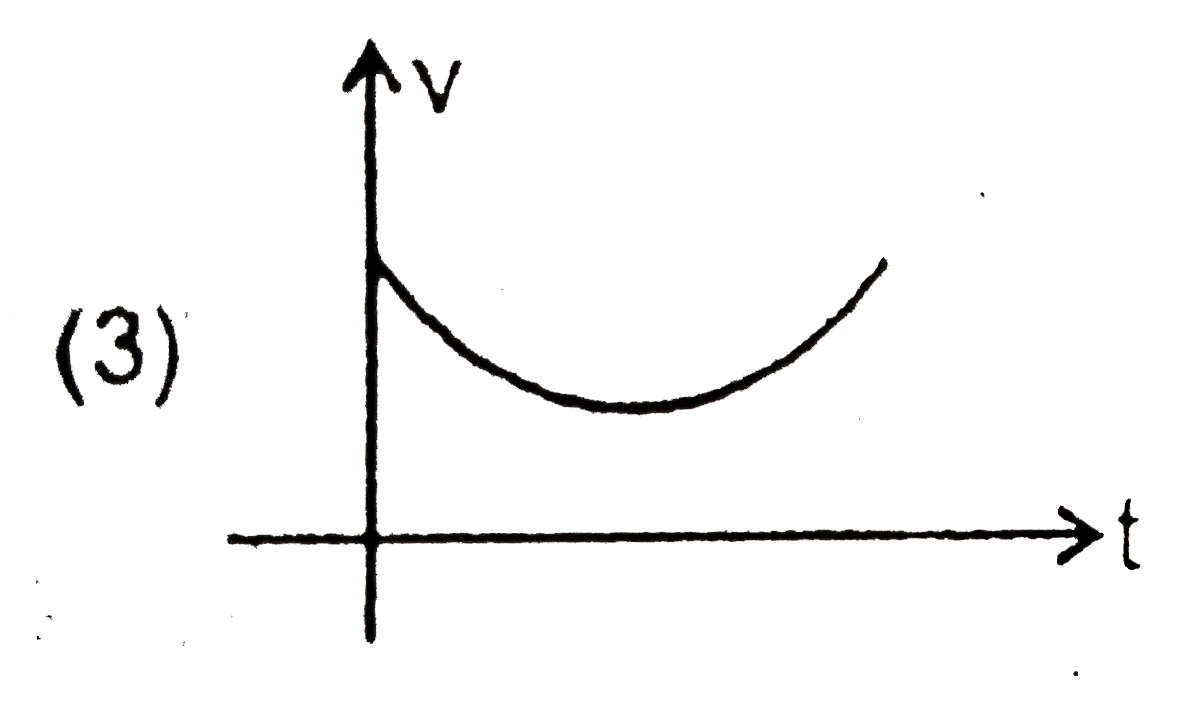
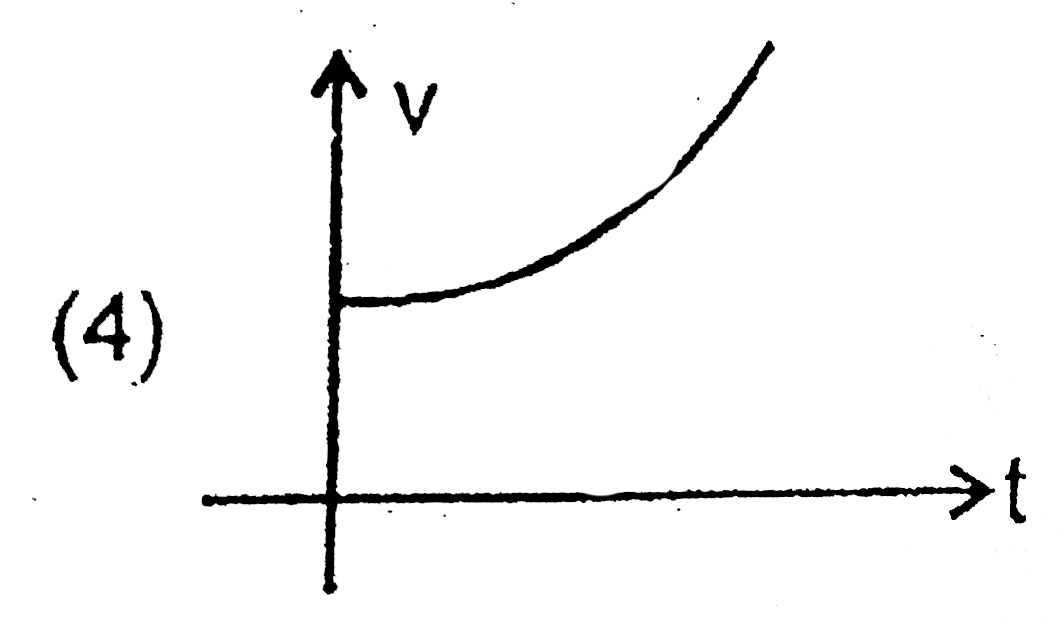
The correct Answer is:B
If a stone ……….
Equation of motion of a particle after time t from moment of projection is:
v=v0−gt (straight line)
Similar Questions
A stone is dropped from a balloon rising upwards with a velocity of 16ms−1. The stone reaches the ground in 4 s. Calculate the height of the balloon when the stone was dropped.
View SolutionA stone is dropped from a ballon rising upwards with a velocity of 16ms−1. The stone reached the ground in 4s. Calculate the height of the ballon when the stone was dropped.
View Solution
Knowledge Check
- Question 1 - Select One
The orbit velocity of a satellite at a height R above the surface of Earth is v. The escape velocity from the location is
A√2vB2vC4vDnone of these - Question 2 - Select One
When we release a stone from a balloon which ascends with a velocity v and acceleration a, the velocity and acceleration of the stone just after release are :
Av↑⏐,(g+a)⏐↓Bv↑⏐,(g−a)⏐↓Cv↑,g↓Dv↑⏐,(a−g)↑⏐ - Question 3 - Select One
A stone is dropped from a height equal to 3R, above the surface of earth. The velocity of stone on reaching the earth's surface is
A√gR2B√32gRC√2gRD√gR
.A ball is projected upwards from a height h above the surface of the earth with velocity v .The time at which the ball strikes the ground is
View SolutionA stone is dropped from a balloon ascending with v0=2ms, from a height h=4.8 m .Find the time of flight of the stone.
View SolutionA stone is thrown vertically upwards with a velocity of 4.9ms−1. Calculate : the time taken to reach the maximum height.
View SolutionA stone is dropped from a height equal to nR, where R is the radius of the earth, from the surface of the earth. The velocity of the stone on reaching the surface of the earth is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View Solution

