If a particle with a=kv2 and initial velocity is u then velocity after S displacement. Here k is a constant
ueks
2ueks
ue2ks
2ue2ks
The correct Answer is:A
If a particle …………..
a=dVdt
vdvds=kv2
∫dvv=k∫ds
lnv=ks+c
at s=0, v=u
⇒lnv=ks+lnu
⇒ln(V)u=ks⇒v=ueks
Similar Questions
[" The acceleration "a" of a particle moving with an initial velocity "u" varies "],[" with distance "x" as "a=k sqrt(x)" where "k" is a constant.The distance covered by "],[" the particle when its velocity becomes "3u" is given by "]
View SolutionVelocity of a particle at time t=0is2m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View Solution
Knowledge Check
- Question 1 - Select One
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A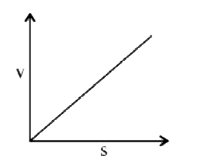 B
B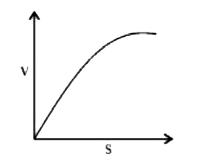 C
C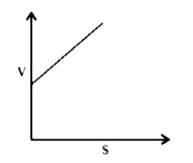 D
D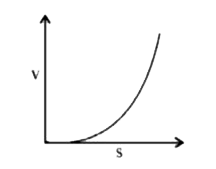
- Question 2 - Select One
Forces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
AKVtBK2V2t2CK2VtD3Kt2V - Question 3 - Select One
A force exerts an impulse Ion a particle changing its speed from initial velocity u to final velocity 2u. The applied force and the initial velocity are oppositely oriented along the same line. The work done by the force is
A32IuB12IuCIuD2Iu

For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positiveView SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionA particle moves with an initial velocity v0 and retardation alphav, where alpha is a constant and v is the velocity at any time t. If the particle is at the origin at t=0, find
(a) (i) velocity as a function of time t.
(ii) After how much time the particle stops?
(iii) After how much time velocity decreases by 50%?
(b) (i) Velocity as a function of displacement s.
(ii) The maximum distance covered by the particle.
(c ) Displacement as a function of time t.View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :View SolutionA constant force F is applied to a body of mass m moving with initial velocity u. If after the body undergoes a displacement S its velocity becomes v, then the total work done is
View Solution

