A particle of mass 1 kg has a velocity of . A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
The correct Answer is:A
Force acting on the particle is constant. Hence, acceleration of the particle will also remain constant.
Since, acceleration is constant. We can apply
and
Refer Fig. 6.17 (a)
Here, u and a t are two mutually perpendicular vectors. So,

Thus, velocity of the particle at the end of is at an angle of with its initial velocity.
Refer Fig.(b)
Here, and are also two mutually perpendicular vectors. So,
and
Thus, displacement of the particle at the end of is at an angle of from its initial velocity.
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Example Type 1
Explore 1 Video
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Example Type 2
Explore 1 Video
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
Velocity of a particle at time t=0is2m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View SolutionA charged particle of charge 2μC and mass 10 milligram, moving with a velocity of 1000m/s enters a uniform electric field of strength 103N/C directed perpendicular to its direction of motion. Find the velocity and displacement of the particle after 10s.
View Solution
Knowledge Check
A constant force F acts for 1 sec, on a body of mass 1kg moving with perpendicular to its initial velocity, then
Adistance covered by the body is (u+F2)Bdisplacement of the body is √u2+(F2)2Cchange in kinetic energy of the body is √12(u2+F2)Dmomentum of the body is increased by F/2.Velocity of a particle at time t=0 is 2ms−1. A constant acceleration of 2ms−2 acts on the particle for 1second at an angle of 60∘ with its initial velocity. Find the magnitude of velocity at the end of 1second.
A√3m/sB2√3m/sC4m/sD8m/sA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.
 A45ms−1B50ms−1C40ms−1D60ms−1
A45ms−1B50ms−1C40ms−1D60ms−1
A particle of mass 1kg is moving with a velocity of 200 m/s. An impulsive force of 4 s duration acts on the particle in a direction opposite to its motion. The force fluctuates a little bit around 40 N magnitude and then it dies out in next 4s showing small fluctuations. An oscilloscope records the force as shown. The two oscillating components in the graph are identical except that one is mirror image of the other. Find the magnitude of velocity of particle after the force stops acting.
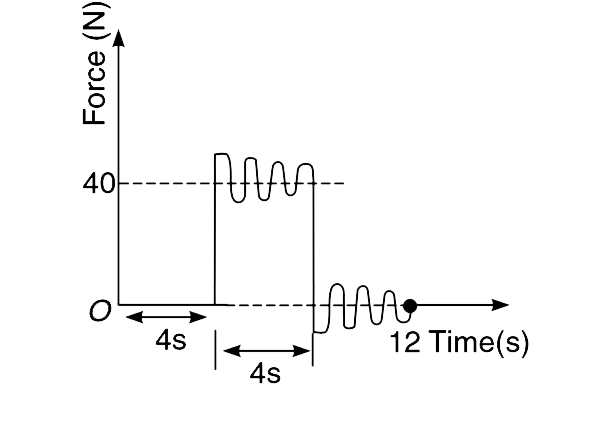
View SolutionA particle of mass 5kg is moving with a velocity of 5ms along a straight line PQ. A force of 12N acts at right angles to PQ on the particles for 3s .Find the velocity of particle at the end of 3sec
View SolutionA particle is projected from ground with velocity 40(√2)m/sat45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle is projected vertically upwards with an initial velocity of 40m/s. Find the displacement and distance covered by the particle in 6s. Take g=10m/s2.
View SolutionIf a particle with a=kv2 and initial velocity is u then velocity after S displacement. Here k is a constant
View Solution