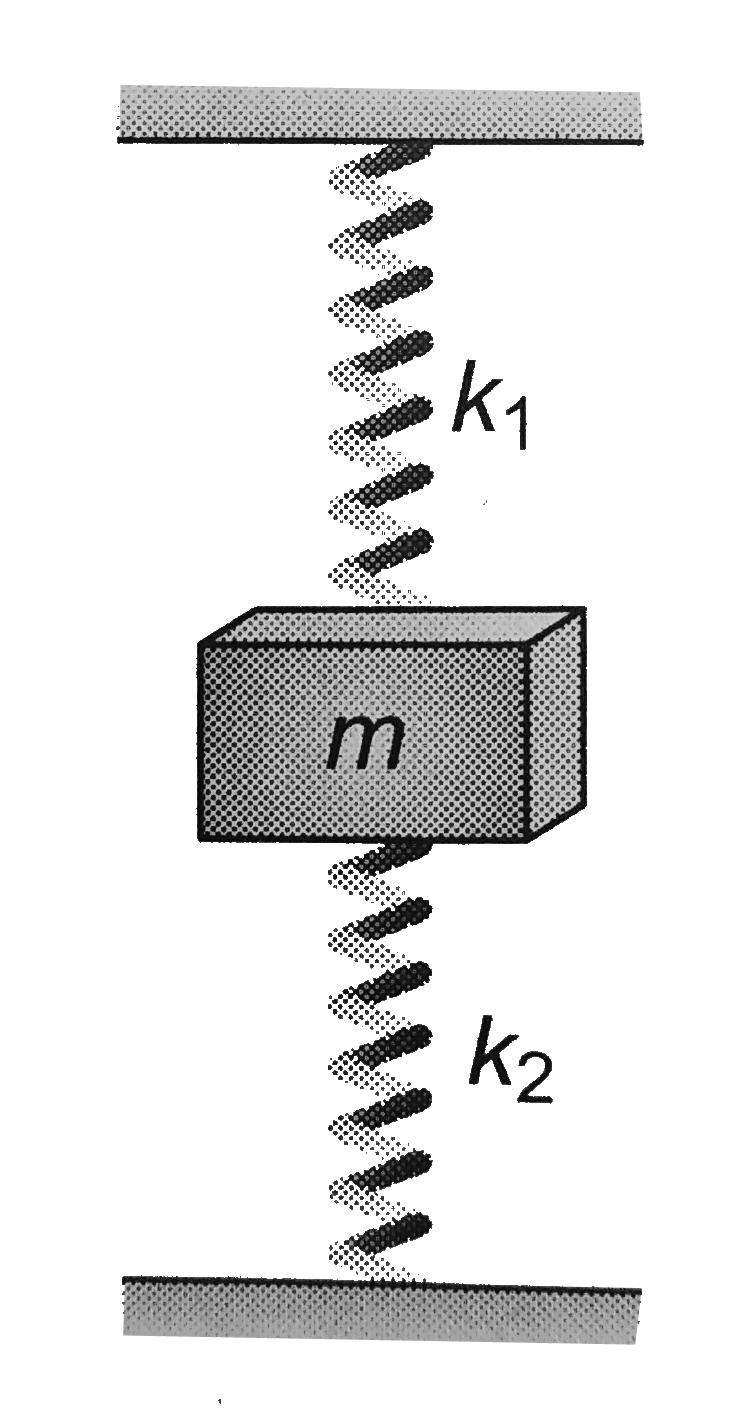
Two springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :

k1k2k1+k2(x1+x2)
k1x1+k2x2
k1x1
None of these
The correct Answer is:C
Tension both springs are same
i.e., k1x1=k2x2=mg= force exerted by lower spring on the block.
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Physics
Explore 775 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of theseA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
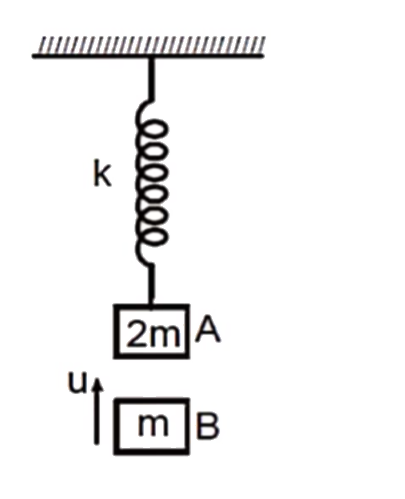
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View Solution