. Let A be the centre of the circle x2+y2−2x−4y−20=0 Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD
The correct Answer is:5
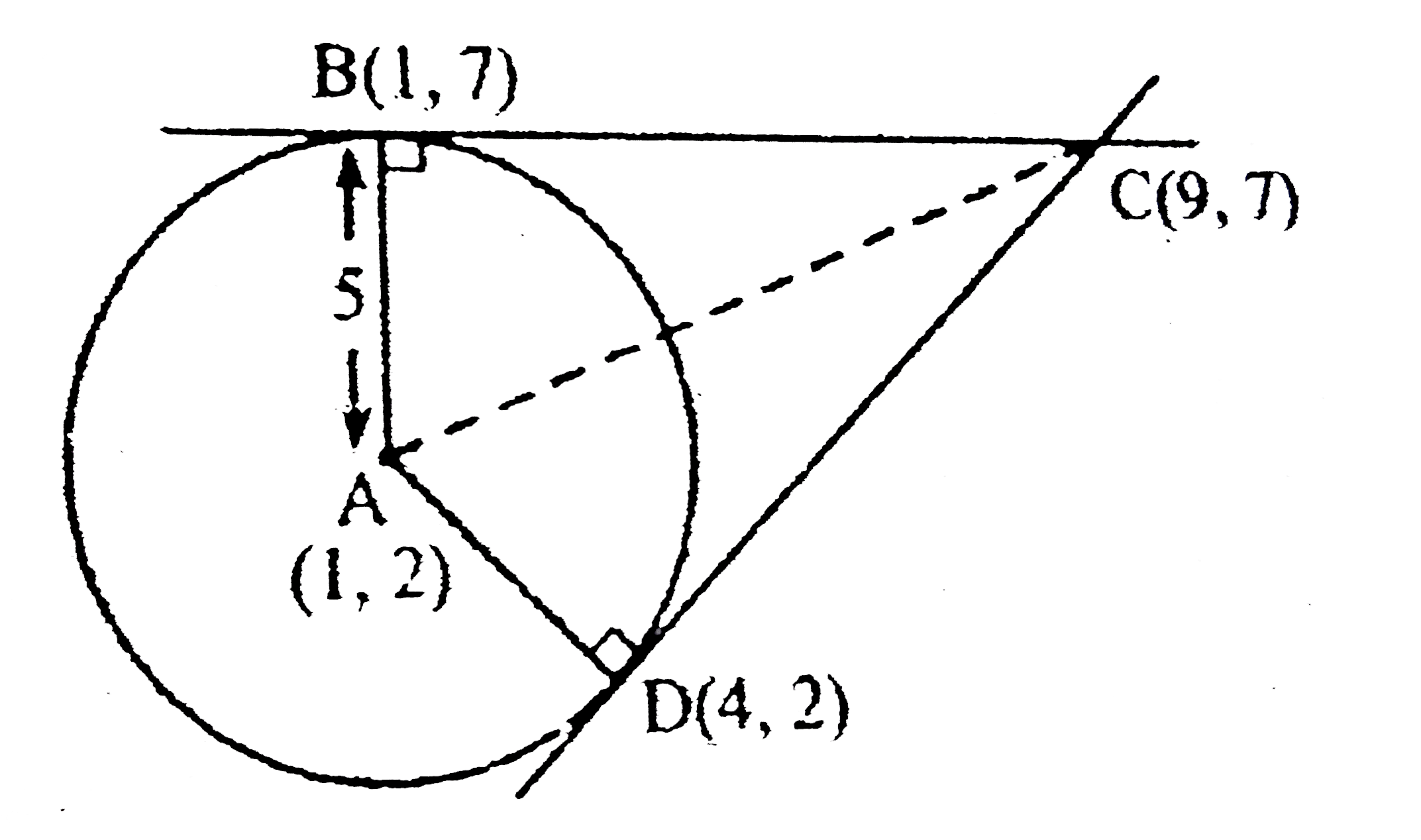
AB is a segment parallel to y− axis and therefore tangent at
B will be parallel to x− axis.
⇒C=(a,7)
Using DC=BC, we get C=(16,7)
⇒BC=15
So that Area (ΔABC)=752
⇒ Area of quadrilateral =75
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Math
105 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
263 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - I MATHEMATICS SEC - 2
1 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS
131 Videos
Similar Questions
Let A be the centre of the circle x2+y2−2x−4y−20=0 .The tangents at the points B(1,7) and C(4,-2) on the circle meet at the point D .If Δ denotes the area of the quadrilateral ABCD,then Δ25 is equal to
View Solution. Let A be the centre of the circle x2+y2−2x−4y−20=0 Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD
View Solution
Knowledge Check
Let A be the centre of the circle x2+y2−2x−4y−20=0. If the tangents at the points B (1, 7) and D(4,−2) on the circle meet at the point C, then the perimeter of the quadrilateral ABCD is
A60 unitsB20 unitsC40 unitsD50 unitsLet A be the centre of the circle x2+y2−2x−4y−20=0 .If the tangents at the points B(1,7)andD(4,-2) on the circle meet at C , then find the area of the quadrilateral ABCD .
A78B75C79D85
The tangent of the circle x2+y2−2x−4y−20=0 at (1,7) meets the y -axis at the point
View SolutionLet B the centre of the circle x2+y2−2x+4y+1=0. Let the tangents at two points P and Q on the circle intersect at the point A(3, 1). Then 8.(area ΔAPQarea ΔBPQ) is equal to ________.
View SolutionAt what points on the circle x2+y2−2x−4y+1=0 , the tangent is parallel to the x-axis.
View SolutionTo the circle x2+y2+8x−4y+4=0 tangent at the point θ=π4 is
View SolutionFind the points on the circle x2+y2−2x+4y−20=0 which are the farthest and nearest to the point (−5,6).
View SolutionFind the points on the circle x2+y2−2x+4y−20=0 which are farthest and nearests to point (-5,6).
View Solution