A body is executing SHM under the action of force whose maximum magnitude is 5√2N. The magnitude of force acting on the particle at the instant when its kintentic energy and potential are euqal is 10x. Find x. (Assume potenital energy to be zero at mean position)
The correct Answer is:5
Fmax=mω2A=50√2
KE=PE at X=A√2
F=mω2A√2=50
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics
775 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A body is executing SHM under the action of force whose maximum magnitude is 50N. Find the magnitude of force acting on the particle at the time when its energy is half kinetic and half potential.
View SolutionForce acting on a particle is F=−8x in S.H.M. The amplitude of oscillation is 2 (in m) and mass of the particle is 0.5 kg. The total mechanical energy of the particle is 20 J. Find the potential energy of the particle in mean position (in J).
View Solution
Knowledge Check
A body is executing SHM under action of the a force of whose maximum is 50N. magnitude of force acting on the particle at the time when its energy is half kineic energy and half potential is (Assume potential energy to be zero at mean position).
A12.5√2NB12.5NC25ND25√2NA body of mass 200 g is executing a S.H.M. of amplitude 50 cm and period 1 s. The magnitude of maximum force acting on the particle is (use π2=10)
A1 NB2 NC3 ND4 NA particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
AForce acting on the particle will be 2FBpotential energy of the particle will be 4U.Cvelocity of particle must be √45vDkinetic energy of particle will be 0.8 K
The potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
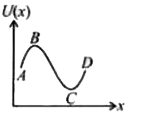
View SolutionThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at

View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View SolutionThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
View Solution
