Rain is falling with constant and uniform velocity v at angle 37∘ vertical. An observer starts from rest and moves with uniform acceleration 2m/s2 in horizontal direction (with the rain). After 6sec. Velocity of rain drop again appear at angle 37∘ from vertical. If velocity of rain fall w.r.t. ground is 5n, then n is : (tan37∘=3/4)
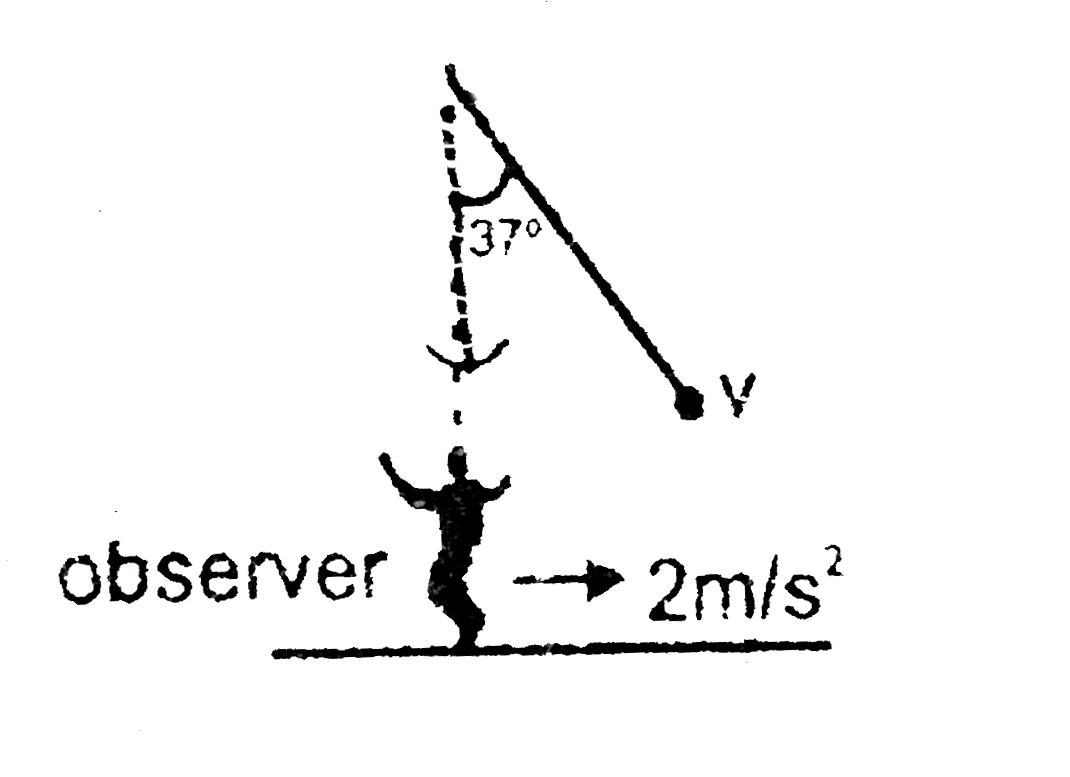
The correct Answer is:2
w.r.t observer
let final velocity of rain be v'
initial velocity of rain =3v5ˆi−4v5ˆj

acceleration of rain =−2ˆjm/s2
final velocity of rain =−3v'5ˆi−4v'5ˆj
in y−direction
vyfinal=vyinitial
v'=v
in x−direction
vyfinal=vyinitial+at
−3v'5=3v5−2⋆6
−3v5=3v5−12
v=10m/s
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics
775 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A man running on a horizontal road at 6km/h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37∘ with the vertical. Find the velocity of rain with respect to the ground.
View SolutionA man is walking due west with a velocity 3km/h and rain appears to be falling vertically with a velocity 4km/h. Find the velocity of rain with respect to the ground.
View Solution
Knowledge Check
A man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hrB5 km/hrC4/3 km/hrD3/4 km/hrA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
Auˆi−utanθˆjBuˆi−ucotθˆjCuˆi+ucotθˆjDutanθˆi−uˆjA stationary man observes that the rain is falling vertically downwards. When he starts running a velocity of 12kmh−1, he observes that the rain is falling at an angle 60∘ with the vertical. The actual velocity of rain is
A12√3kmh−1B6√3kmh−1C4√3kmh−1D2√3kmh−1
A man when standstill observes the rain falling vertically and when he walks at 4km/h he has to hold his umberella at an angle 53∘ from the vertical. Find velocity of the raindrops.
View SolutionA man is walking on a road with a velocity 3kmhr. Suddenly rain starts falling. The velocity of rain is 10km/hr in vertically downward direction. the relative velocity of rain with respect to man is :-
View SolutionA standing man observes rain falling with the velocity of 20ms−1 at an angle of 30∘ with the vertical.
(a) Find the velocity with which the amn should move so that rain appears to fall vertically to him.
Now if he futher increases his speed, rain again appears to fall at 30∘ with the vertical. Find his new velocity.
View SolutionA man is standing on a road and observes that rain is failing at angle 45∘ with the vertical. The man starts running on the road with constant acceleration 0.5m/s2. After a certain time from the start of the motion, it appears to him that rain is still falling at angle 45∘ with the vertical, with speed 2√2m/s. Motion of the man is in the same vertical plane in which the rain is falling. Then which of the following staement(s) are true.
View SolutionIt is raining at a speed of 5m/s−1 at an angle 37∘ to vertical, towards east.A man is moving to west with a velocity of 5m/s−1.The angle with the vertical at which he has to hold the umbrella to protect himself from rain is.
View Solution