Touching a hemispherical dome of radius R there is a vertical tower of height H=4r. A boy projects a ball horizontally at speed u from the top of the tower. The ball strikes the dome at a height R2 from ground and rebounds. After rebounding the ball retraces back its path into the hands of the boy. Then the value of u is :
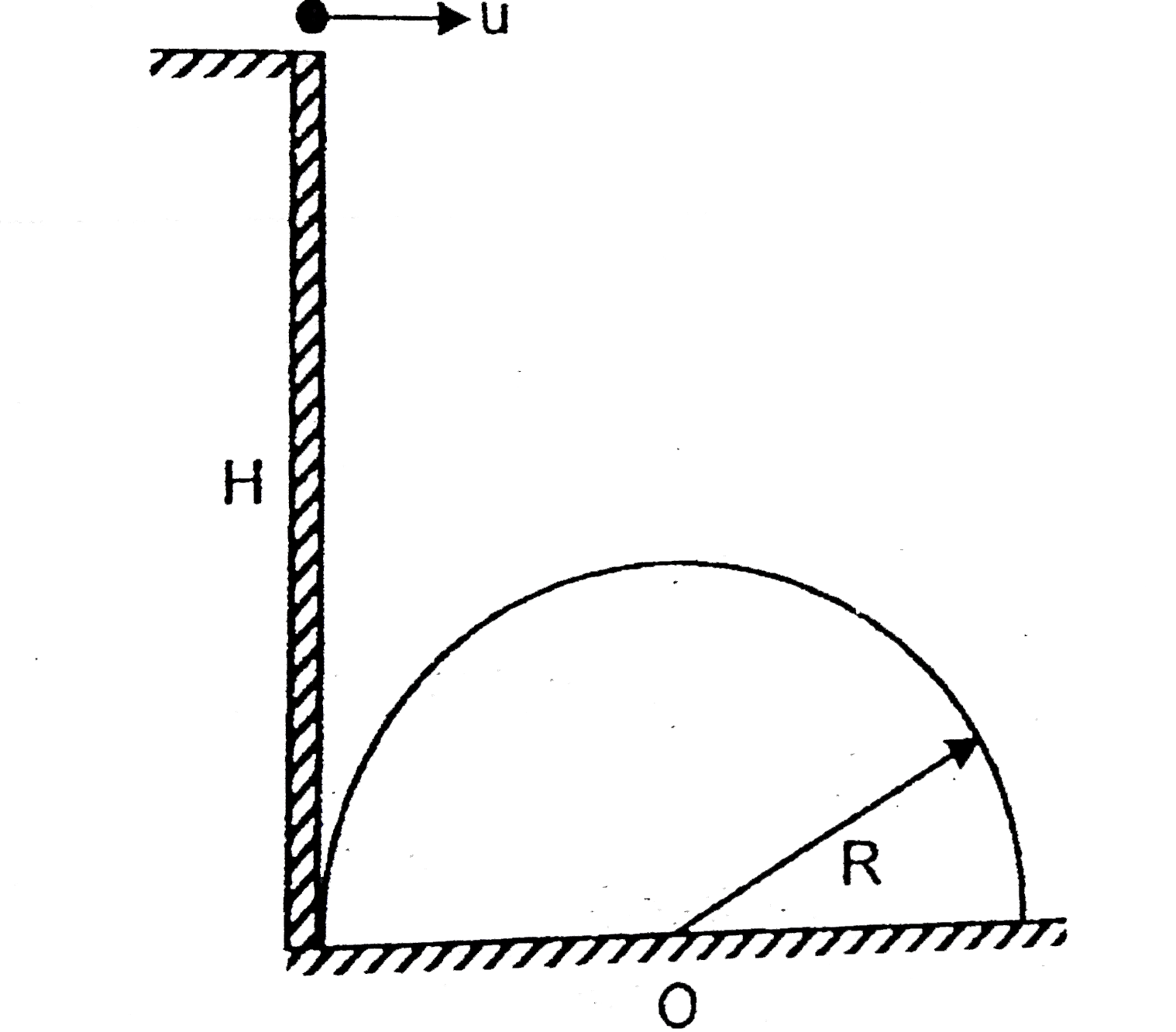
√20gR
√21gR
√17gR
None of these
The correct Answer is:B
The ball must strike the sphere normally (i.e. along radius) so that is can rebound back along the same path
sinθ=R/2R=12
θ=30∘
The velocity of the ball at the instant of hitting the sphere is inclined at θ to the horizontal
∴tanθ=vyvx
1√3=√2g(7R2)u
∴u=√21gR

Similar Questions
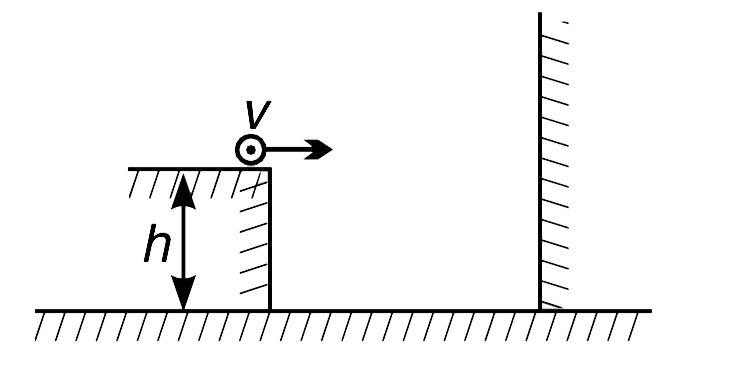
(a) A particle is thrown from a height h horizontally towards a vertical wall with a speed v as shown in the figure. If the particle returns to the point of projection after suffering two elastic collisions, one with the wall and another with the ground, find the total time of flight. [Elastic collision means the velocity component perpendicular to the surface gets reversed during collision.]
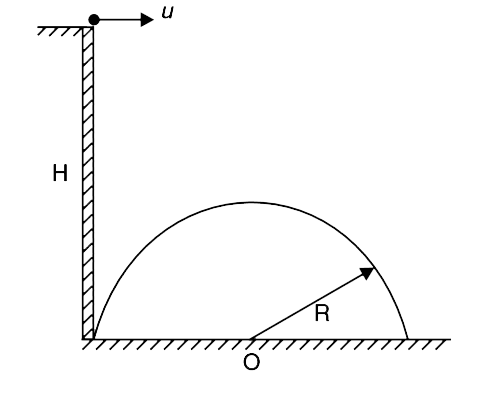
(b) Touching a hemispherical dome of radius R there is a vertical tower of height H=4R. A boy projects a ball horizontally at speed u from the top of the tower. The ball strikes the dome at a height R2 from ground and rebounds. After rebounding the ball retraces back its path into the hands of the body. Find u.
View SolutionA body is projected vertically upwards with speed u from the top of a tower. It strikes at the ground with speed 3u. What is (a) height of tower and (b) time take by the body to reach at the ground?
View Solution
Knowledge Check
A ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
Avg[1+√1+2ghv2]Bvg[1+√1−2ghv2]Cvg(1+2ghv2)1/2Dvg(1−2ghv2)1/2A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Time taken by the ball to strike the ground isA√20sB2√20sC4√20sD10sA ball throuwn vertically upwards with a speed of 19.6ms−1 from the top of a tower returns to the earth in 6s. Find the height of the tower.
A40 mB58.8 mC50 mD70 m
A ball is thrown upwards with speed v from the top of a tower and it reaches the ground with speed 3v .The height of the tower is
View SolutionA ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
velocity with which the ball strikes the ground is .
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View SolutionA ball is thrown vertically upwards from the top of a tower at 4.9ms−1 . It strikes the pond near the base of the tower after 3 seconds . The height of the tower is
View SolutionA ball projected upwards from the foot of a tower. The ball crosses the top of the tower twice after an interval of 6s and the ball reaches the ground after 12s. The height of the tower is (g=10m/s2) :
View Solution
