Two hemispheres of radii and are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is . Then the maximum value of the ratio for which the rod will not slide is :

None of these
The correct Answer is:A

In figure
[where]………(1)
The equilibrium of rod gives
…..(2)
and .......(3)
Assuming the friction to be at its limiting value.
gives
Put in
If the ratio is decreased, wil increase and the rod will begin to slide.

Similar Questions
A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View Solution
Knowledge Check
The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
AR2B(1−√32)RC√32RD3R8Two metal spheres of radii R1 and R2 are charged to the same potential. The ratio of charges on the spheres is
A√R1:√R2BR1:R2CR21:R22DR31:R32
A rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
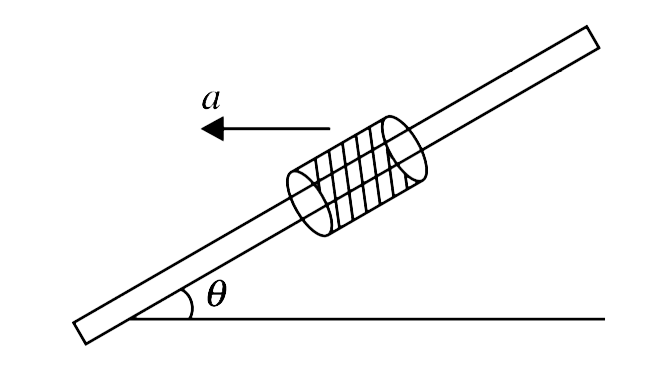
View SolutionA hemisphere of mass M and radius R rests on a smooth horizontal table. A vertical rod of mass m is held between two smooth guide walls supported on the sphere as shown. There is no friction between the rod and the sphere. A horizontal string tied to the sphere keeps the system at rest.
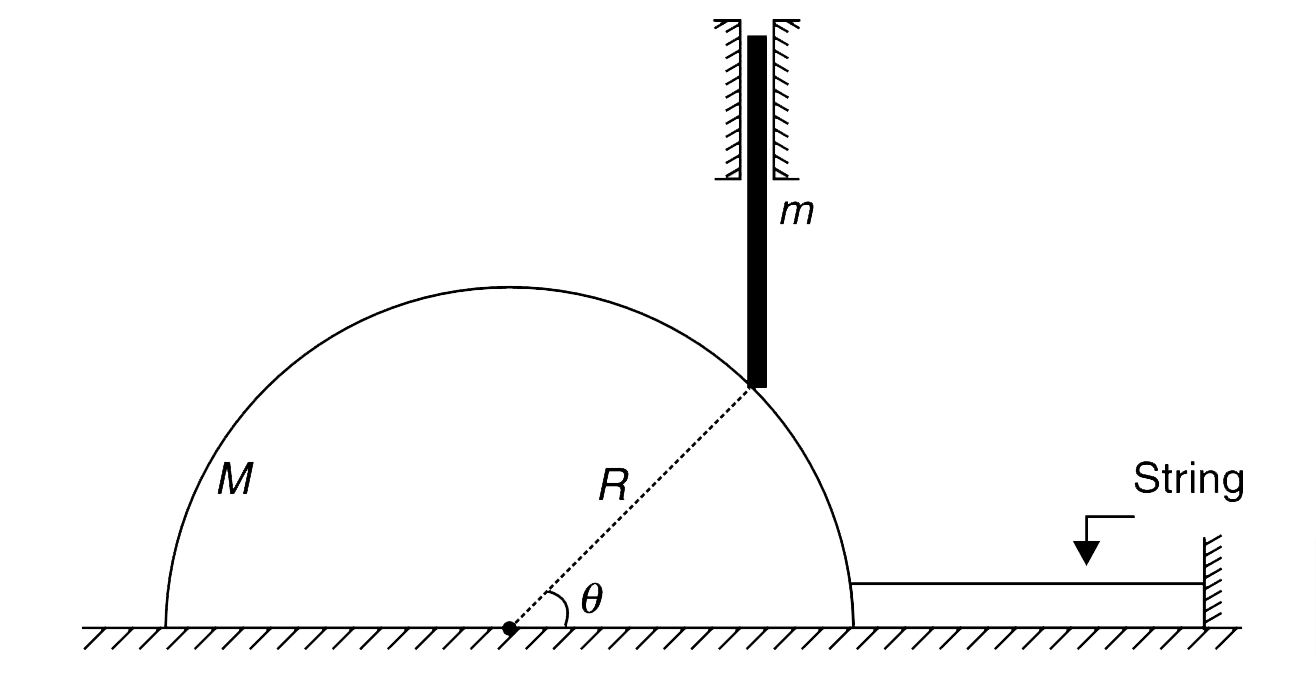
(a) Find tension in the string.
(b) Find the acceleration of the hemisphere immediately after the string is cut.
View SolutionA uniform rod is held at an angle of 45∘ to the horizontal and released from rest as shown. The minimum coefficient of friction between plane and rod required so that the rod does not slip on the plane upon releases, will be

View SolutionTwo speres of radii r and 2r touching each other the force of attraction betweeen them is proportional
View SolutionTwo spheres of radii R1 and R2 are made of the same material and are at the same temperature. The ratio of their thermal capacities is:
View Solution
