Sum of all the numbers that can be formed using all the digits 2,3,3,4,4,4 is
11111100
22222200
55555500
20333280
The correct Answer is:B
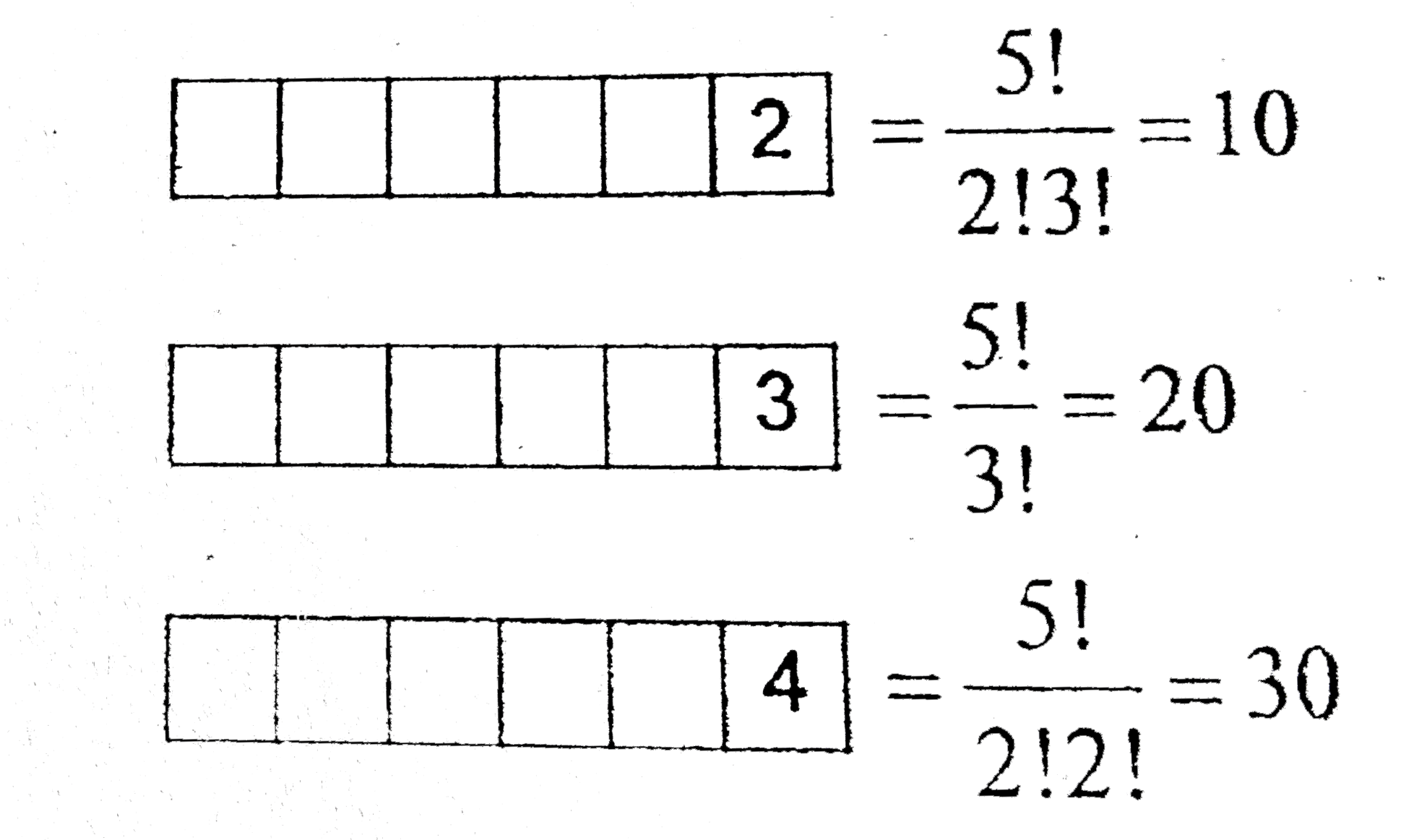
∴sum=(2×10)+(3×20)+(4×30)=200
of unit place
∴ Reqd. sum
=200(105+104+103+102+101+100)
=200(111111)=22222200
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Video
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS
131 Videos
Similar Questions
Knowledge Check
What is the sum of all three-digit numbers that can be formed using all the digits 3, 4 and 5, when repetition of digits is not allowed ?
A2664B3882C4044D4444What is the sum of all three-digit numbers that can be formed using all the digit 3,4 and 5, when repetition of digits is not allowed?
A2664B3882C4044D4444The sum of all five-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 when repetition of digits is not allowed, is
A366000B660000C360000D3999960
The sum of all the numbers which can be formed by using the digits 1, 3, 5, 7 all at a time and which have no digit represented, is
View SolutionSum of all the 4-digit numbers which can be formed using the digits 0, 3, 6, 9 (without repetition of digits) is 119988 (b) 115992 (c) 3996 (d) None of these
View SolutionHow many numbers can be formed using the digits 1, 2, 3, 4, 3, 2, 1 so that the odd digits always occupy the odd places?
View SolutionThe number of different numbers that can be formed by using all the digits 1, 2, 3, 4,3, 2,1 so that odd digits always occupy the odd places IS 1) 6 2)72 3) 60 4) 18
View SolutionThe sum of all 4 digit number that can be formed by using the digits 2 ,4, 6 ,8 .
View Solution