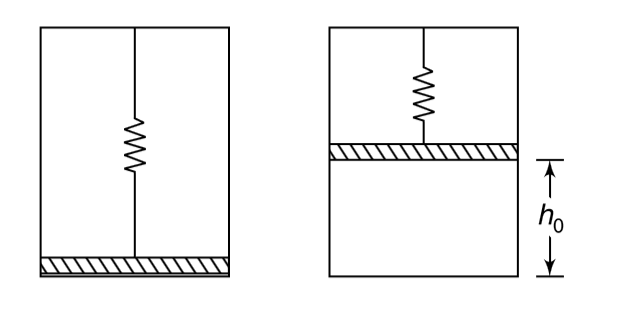
(i) A conducting cylinder whose inside diameter is $4.00 c m$ contains air compressed by a piston of mass $m = 13.0 k g$ , which can slides freely in the cylinder shown in the figure. The entire arrangement is immersed in a water bath whose temperature can be controlled. The syetem is initially in equilibrium at temperature $t_{1} = 20^{\circ} C$ . The initial height of the piston above the bottom of the cylinder is $h_{i} = 4.00 c m . P_{a t m} = 1 \times 10^{5} \frac{N}{m^{2}}$ and $g = 10 m / s^{2}$ .
If the temperature of the water bath is gradually increased to a final temperature $t_{f} = 100^{\circ} C$ . Find teh height $h_{f}$ of the piston (in cm) at that instant?
(ii) In the above question, if we again start from the initial conditions and the temperature is again gradually raised, and weights are added to the piston to keep its height fixed at $h_{i}$ . Find the value of teh added mass when the final temperature becomes $t_{f} = 100^{\circ} C$ ?

Text Solution

Verified by Experts

The correct Answer is:(i) $\frac{1492}{293} c m$
(ii) $\frac{320 π}{293} (1 + \frac{13}{4 π}) k g$

(i) Initial pressure of gas $P_{i} = P_{a t m} + \frac{m g}{A} =$ final pressure
$V_{i} = A h_{i}$ and $V_{f} = A h_{f}$
For air inside cylinder $n_{1} = n_{2} \Rightarrow \frac{P_{i} V_{i}}{T_{i}} = \frac{P_{f} V_{f}}{T_{f}}$
$\Rightarrow h_{f} = \frac{h_{i} T_{f}}{T_{i}} = \frac{4 \times 373}{293} = \frac{1492}{293} c m$
(ii) Here volume is constant $\frac{P_{i}}{T_{i}} = \frac{P_{f}}{T_{f}}$
$m = \frac{P_{a t m} (T_{f} - T_{i}) A + M g (T_{f} - T_{i})}{g T_{i}}$
$= \frac{1 \times 10^{5} (80) π {(2 \times 10^{- 2})}^{2} + 13 (80) \times 10}{10 \times 293}$
$= \frac{320 π}{293} (1 + \frac{13}{4 π}) K g$

Updated on:21/07/2023

|

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

RESONANCE-KTG & THERMODYNAMICS-SECTION

Home
Ask Doubt
Profile