S is a piston of mass M which can slide inside a cylinder without friction. The walls of the cylinder is adiabatic and the piston is diathermic and area of cross section of cylinder is A. Length of the cylinder is 2l0. Initial pressure of each chamber is P0. Volume of the chambers are equal. Initially spring is unstretched and has spring constant k. The spring is fixed with piston and wall of the cylinder as shown in the figure. Find out its time period when piston is given small displacement.
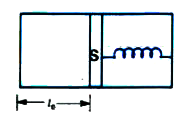
T=2π√MI02P0A+Kl0
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
7 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - Problem
60 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
19 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
The pressure of a gas contained in a cylinder with a movable piston is 300 Pa. The area of the piston is 0.5m2. Calculate the force that is exerted on the piston.
View SolutionA non conducting piston of mass m and area of cross section A is placed on a non conducting cylinder as shown in figure. Temperature, spring constant, height of the piston are given by T,K,h respectively. Initially spring is relaxed and piston is at rest. Find
(a) Number of moles
(b) Work done by gas to displane the piston by distance d when the gas is heated slowly.
(c ) Find the final temperature

View Solution
Knowledge Check
In the cylinder shown in the figure, air is enclosed under the piston. Piston mass M=60 kg, crosssectional area of the cylinder S0=20cm2 atmospheric pressure P0=105paα=37∘. The air temperature is constant, the friction is negligible.

What is the pressure of the enclosed gas?A3.4×105 PaB4×105 PaC4.75×105 PaD2.8×105 PaA ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
A2π√BA2MV0B2π√BAMV20C2π√BAMV0D2π√B2AMV0A closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston isAP0γA2xV0B2P0γA2xV0C3P0γA2xV0DP0γA2x(γ−1)V0
A non conducting piston of mass m and area of cross section A is placed on a non conducting cylinder as shown in figure. Temperature, spring constant, height of the piston are given by T,K,h respectively. Initially spring is relaxed and piston is at rest. Find
(a) Number of moles
(b) Work done by gas to displaced the piston by distance d when the gas is heated slowly.
(c ) Find the final temperature

View SolutionMethod 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

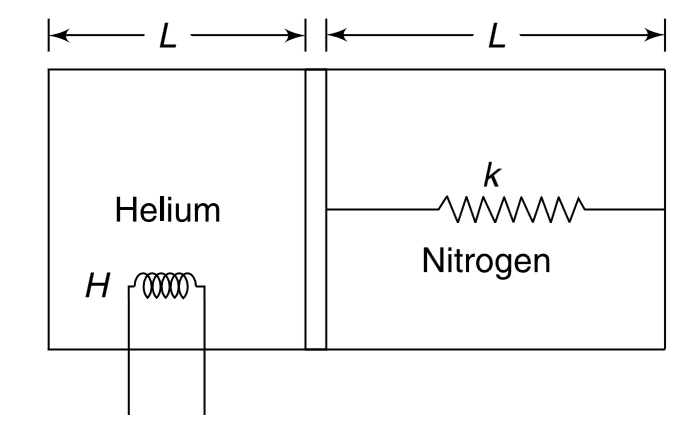
View SolutionAn adiabatic cylinder has length 2 L and cross sectional area A. A freely moving non conducting piston of negligible thickness divides the cylinder into two equal parts. The piston is connected to the right face of the cylinder with an ideal spring of force constant k. The right chamber contains 28 g nitrogen in which one third of the molecules are dissociated into atoms. The left chamber container 4 g helium. With piston in equilibrium and spring relaxed the pressure in both chamber is P0. The helium chamber is slowly given heat using an electric heater (H), till the piston moves to right by a distance 3L4. Neglect the volume occupied by the spring and the heating coil. Also neglect heat capacity of the spring.
(a) Find the ratio of CP and CV for nitrogen gas in right chamber.
(b) Calculate change in temperature of helium.
(c) Calculate heat supplied by the heater.
View SolutionAir is contained in a piston-cylinder arrangement as shown in Fig. with a cross-sectional area of 4cm2 and an initial volume of 20. The air is initially at a pressure of 1 atm and temperature of 20∘C. The piston is connected to a spring whose spring constant is k=104N/m, and the spring is initially underformed. How much heat must be added to the air inside cylinder to increase the pressure to 3 atm (for air, CV=718J/kg.∘C, molecular of air 28.97)?

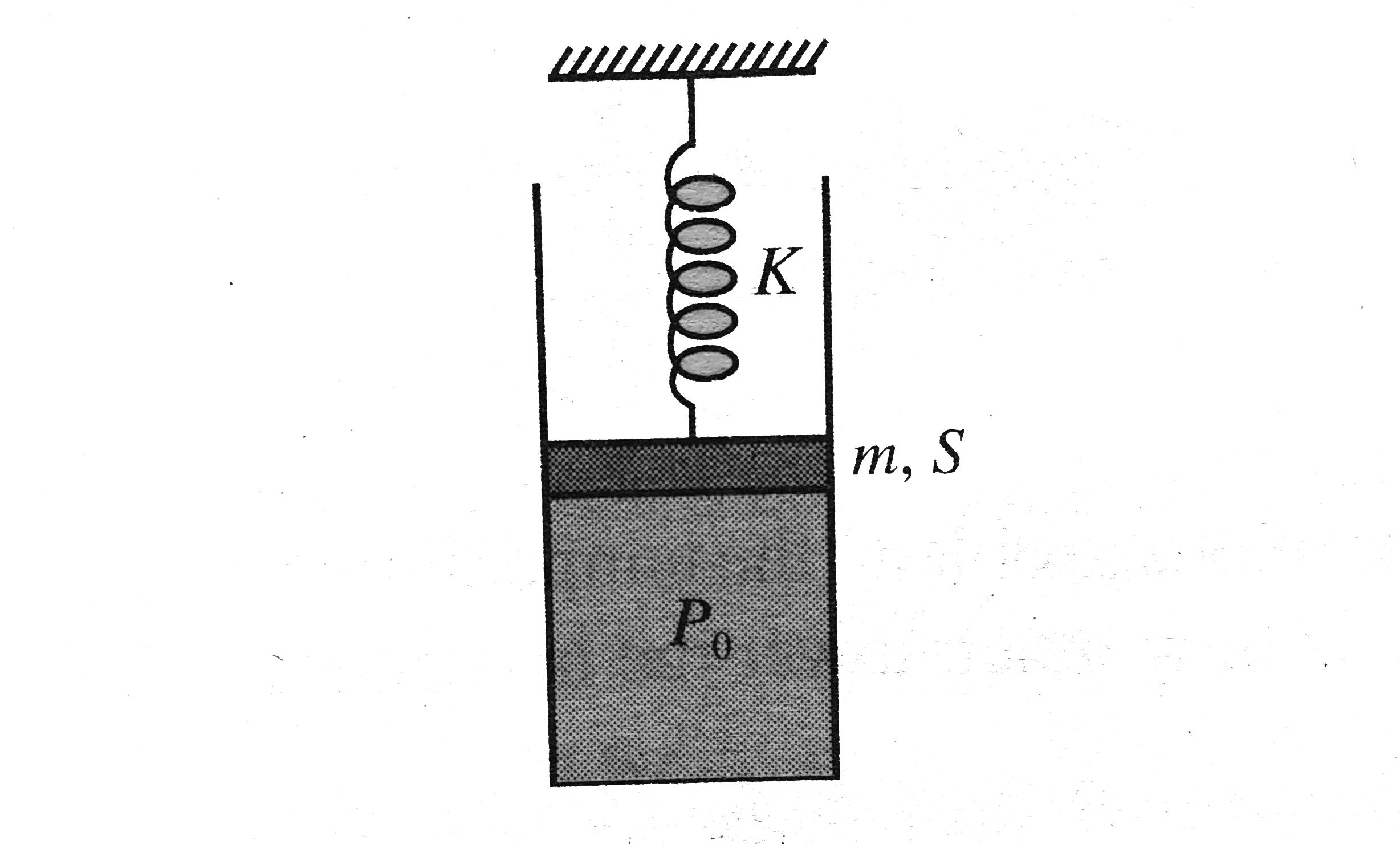
View SolutionIn the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P0 (gt atmospheric pressure P0). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x0, then
View Solution
