Temperature of plate is increased by Δθ then find new

inner radius
outer radius
the difference in outer and inner radius and show that it is positive
area of plate meterial (assume coefficient of expansion is α)
The correct Answer is:A, B, C, D
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-2
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-3
1 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-1
1 Videos
- CALORIMETRYBOOK - RESONANCECHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCECHAPTER - CAPACITOREXERCISE - Exercise
45 Videos
Similar Questions
If rod is initially compressed by Δl length then what is the strain on the rod when the temperature
(a) is increased by Δθ (b) is decreased by Δθ
View SolutionIf rod is initially compressed by Δl length then what is the strain on the rod when the temperature
(a) is increased by Δθ (b) is decreased by Δθ
View Solution
Knowledge Check
A square metal plate with a hole is at temperature θ is present on smooth horizontal surface. Point P&C are marked on the plate, where C is centre of mass of the plate with the hole shown. When temperature of the plate is increased then the point.
 AP-shifts towards leftBP shifts towards rightCC shifts towards leftDC shifts towards right
AP-shifts towards leftBP shifts towards rightCC shifts towards leftDC shifts towards rightAn ideal gas is initially at temperature T and volume V. ITS volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔV/VΔT varies with temperature as
A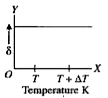 B
B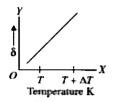 C
C D
D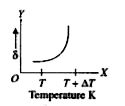
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A B
B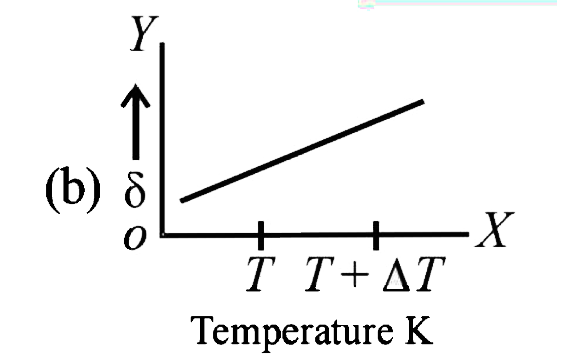 C
C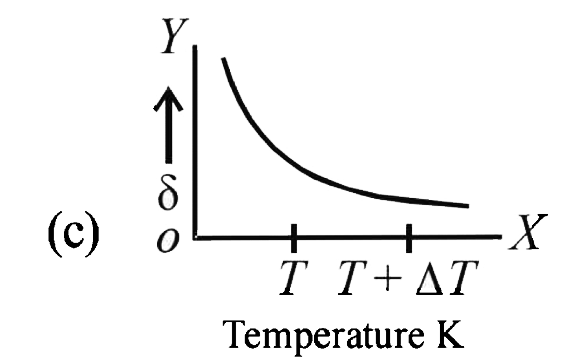 D
D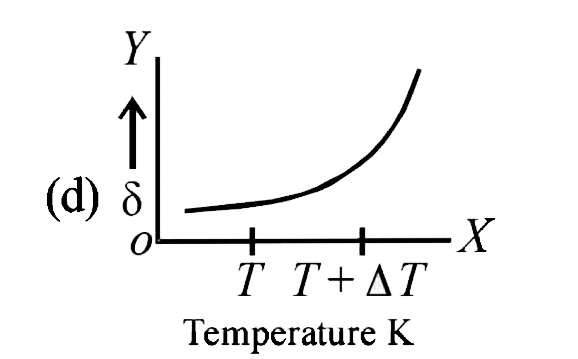
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
View SolutionWhen the temperature of a rod increases from t to r+Δt, its moment of inertia increases from I to I+ΔI. If α is the value of ΔI/I is
View SolutionAn ideal gas is initially at temperature T and volume V . Its volume is increased by ΔV due to an increase in temperature Δ , pressure remaining constant . The quantity δ=ΔV/VΔT varies with temperature as
View SolutionWhen the temperature of a rod increases from t to t+Δt, its moment of inertia increases from I to I+ΔI. If α is coefficient of linear expansion, the value of ΔI/I is
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
View Solution
