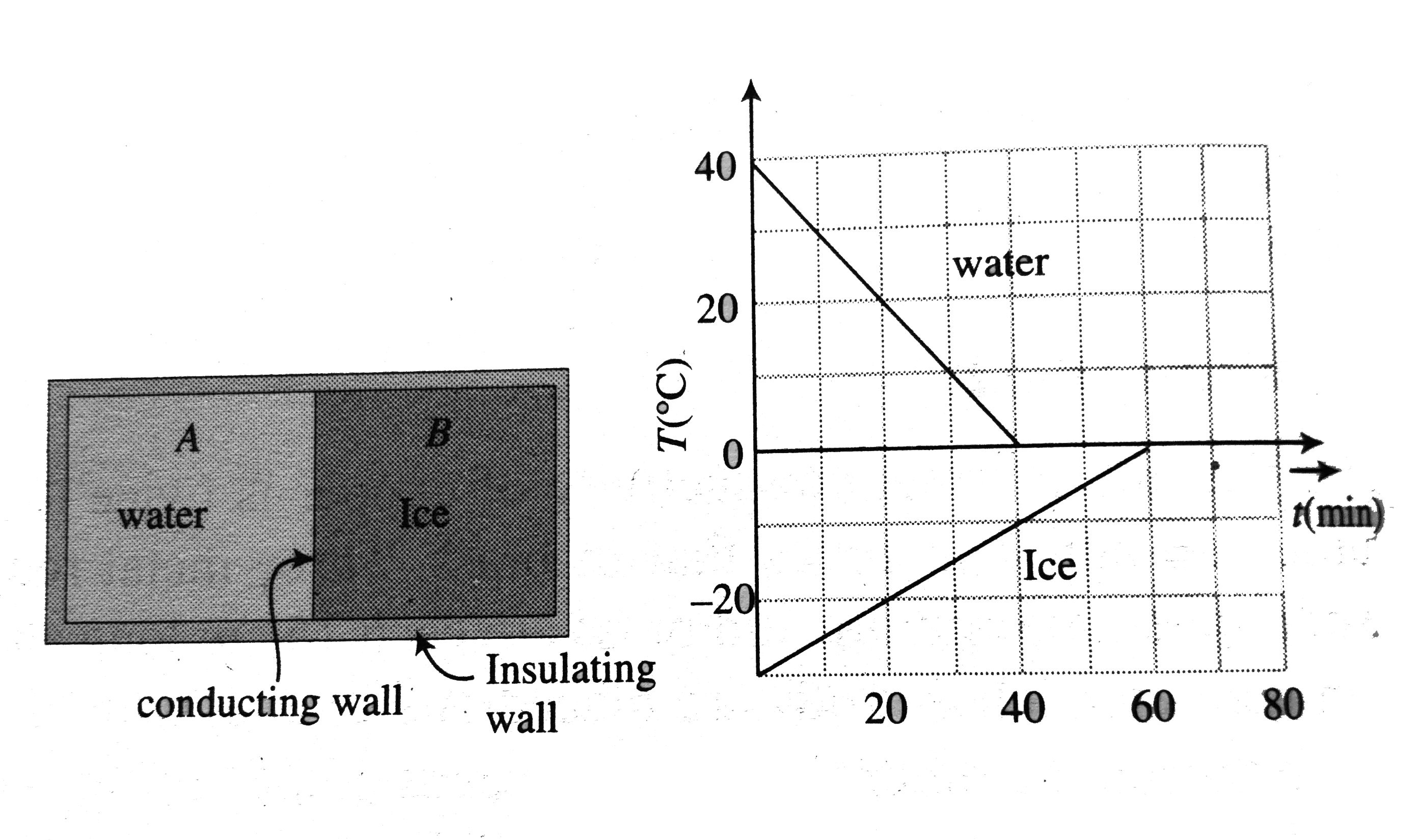
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
42.0W
36.0W
21.0W
18.0W
The correct Answer is:A
Step by step video, text & image solution for A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K, specific heat of water =4200 J//kg-K, and latent heat of fusion of ice =3.3xx10^5 J//kg. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-21videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-31videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCECHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercise-11videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCECHAPTER - CALORIMETRYEXERCISE - Exercise19videos
CALORIMETRY
- BOOK - RESONANCECHAPTER - CAPACITOREXERCISE - Exercise45videos
CAPACITOR
Similar Questions
A metal ball of specific gravity 4.5 and specific heat 0.1cal/gm−∘C is placed on a large slab of ice at 0∘C. Half of the ball sinks in the ice. The initial temperature of the ball is:- (Latent heat capacity of ice =80cal/g, specific gravity of ice =0.9)
08:42View SolutionA cube of coefficient of linear expansion α is floating in a bath containing a liquid of coefficient of volume expansion γl. When the temperature is raised by ΔT, the depth upto which the cube is submerged in the liquid remains the same. Find relation between α and γl
08:42View SolutionIn the following equation calculate the value of H.
1kg syeam at 200∘C=H+1kg water at 100∘C(Ssystem= Constant=0.5cal/gm∘C)08:42View SolutionThe amount of heat required to change the state of 1 kg of substance at constant temperature is called
04:02View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
03:20View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg .
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
03:10View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
06:20View SolutionWater at 10^(@) C is present in a thermally insulated container. Calculate the ratio of mass of ice formed and initial mass of water, if a small crystal of ice is thrown into it.
View SolutionIn an 20 m deep lake, the bottom is at a constant temperature of 4∘C. The air temperature is constant at −10∘C. The thermal conductivity of ice in 4 times that water. Neglecting the expansion of water on freezing, the maximum thickness of ice will be
View SolutionPure water cooled to −15∘C is contained in a thermally insulated flask. Some ice is added into the flask. The fraction of water frozen into ice is :
View Solutionপুকুরের জলের ওপর 5cm পুরু বরফ রয়েছে। বরফের ওপর বায়ুর তাপমাত্রা -10°C। কি হারে প্রতি বর্গ সেন্টিমিটার ক্ষেত্রফলের ভিতর দিয়ে বরফ তাপ পরিবাহিত করবে? বরফের তাপ পরিবাহিতাঙ্ক =5×10−3 CGS unit।
01:50View Solution(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at 25^(@)C , and the ice comes directly from a freezer at - 15^(@)C , what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
04:08View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process. Given, specific heat of ice = 2100 J/kg-K Specific heat of water = 4200 J/kg-K latent heat of fusion of ice = 3.3 xx 10^(-5) J/kg The value of rate P is
02:33View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process.
Given, specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
latent heat of fusion of ice = 3.3×10−5 J/kg
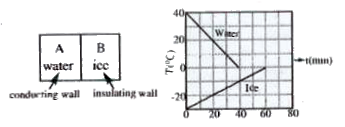
The initial mass of the ice in the container is equal to02:49View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process. Given, specific heat of ice = 2100 J/kg-K Specific heat of water = 4200 J/kg-K latent heat of fusion of ice = 3.3 xx 10^(-5) J/kg The mass of the ice formed due to conversion from hte water till thermal equilibrium is reached , is equal to
03:58View Solution

