Calculate thermal conductance for radial flow of an annular cylinder of length and inner and outer radius and . Assume that thermal conductivity of the material is

The correct Answer is:

Solving
Topper's Solved these Questions
Similar Questions
Calculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r1and r2. Assume that thermal conductivity of the material is K
View Solution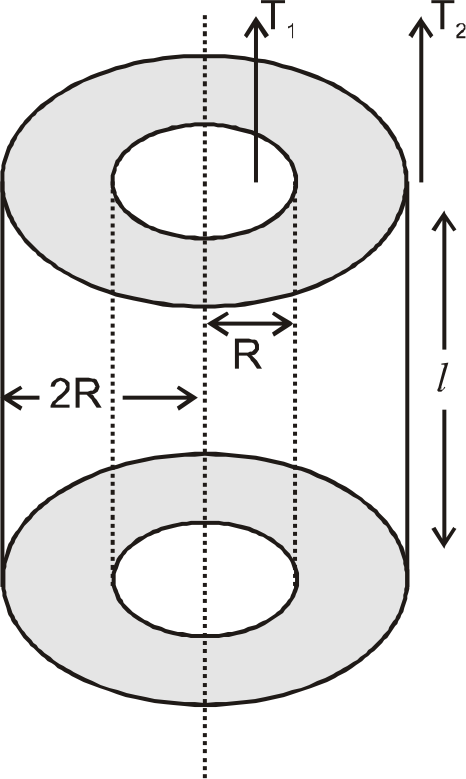
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
View Solution
Knowledge Check
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylinderical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effictive thermal conductivity of the system is
AK1+K2BK1K2/(K1+K2)C(K1+3K2)/4D(3K1+3K2)/4A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
AK1+K2BK1K2K1+K2C√K1K2D2K1K2K1+K2A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
AK1+K2BK1K2K1+K2CK1+3K24D3K1+K24
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2 . The inner surface (a cylinder of length d and radius r1 is maintained at a temperature θ1 and the oouter surface (a cylinder of length d and radius r2 . The is maintianed at a temperature θ2(θ1>θ2) .The thermal conductivity of the material of the dics is K. Calculate the heat flowing per unit time through the disc.
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .
.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionA cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
View Solution
